
5. (2009年威海一中模拟) 如图所示,A为一放在竖直轻弹簧上的小球,在竖直向下恒力F的作用下,在弹簧弹性限度内,弹簧被压缩到B点,现突然撒去力F,小球将向上弹起直至速度为零,不计空气阻力,则小球在上升过程中( D )
(2009年威海一中模拟) 如图所示,A为一放在竖直轻弹簧上的小球,在竖直向下恒力F的作用下,在弹簧弹性限度内,弹簧被压缩到B点,现突然撒去力F,小球将向上弹起直至速度为零,不计空气阻力,则小球在上升过程中( D )
A. 小球向上做匀变速直线运动
B. 当弹簧恢复到原长时,小球速度恰减为零
C. 小球机械能逐渐增大
D. 小球动能先增大后减小
4. (江苏省启东中学月考) 如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑轮O,倾角为30°的斜面体置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( ABC )
(江苏省启东中学月考) 如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑轮O,倾角为30°的斜面体置于水平地面上.A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( ABC )
A.物块B受到的摩擦力先减小后增大
B.地面对斜面体的摩擦力方向一直向右
C.小球A的机械能守恒
D.小球A的机械能不守恒,A、B系统的机械能守恒
3.(2009年山东潍坊一模) 一个质量为m的小铁块沿半径为R 的固定半圆轨道上边缘由静止滑下,到半圆底部时,轨道所受压力为铁块重力的1.5倍,则此过程中铁块损失的机械能 为
( .D )
为
( .D )
A.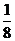 mgR
B.
mgR
B.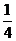 mgR
mgR
C.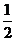 mgR
D.
mgR
D. mgR
mgR
2.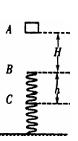 (江苏省铁富中学月考) 如图所示,质量为m的物块从A点由静止开始下落,速度是g/2,下落H到B点后与一轻弹簧接触,又下落h后到达最低点C,在由A运动到C的过程中,空气阻力恒定,则( D )
(江苏省铁富中学月考) 如图所示,质量为m的物块从A点由静止开始下落,速度是g/2,下落H到B点后与一轻弹簧接触,又下落h后到达最低点C,在由A运动到C的过程中,空气阻力恒定,则( D )
A.物块机械能守恒
B.物块和弹簧组成的系统机械能守恒
C.物块机械能减少
D.物块和弹簧组成的系统机械能减少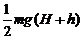
1.(2009广东肇庆高三一模) 质量为m的物体,从静止开始以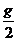 的加速度竖直下落h的过程中,下列说法中正确的是( BD )
的加速度竖直下落h的过程中,下列说法中正确的是( BD )
A.物体的机械能守恒 B.物体的机械能减少
C.物体的重力势能减少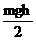 D.物体克服阻力做功为
D.物体克服阻力做功为
2009联考题
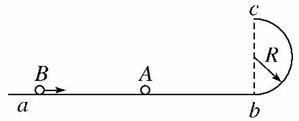
14.(04·安徽春季理综·34)如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30 m,质量m=0.20 kg的小球A静止在轨道上,另一质量M=0.60 kg,速度v0=5.5 m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为l=4 R处,重力加速度g=10 m/s,求:
R处,重力加速度g=10 m/s,求:
(1)碰撞结束后,小球A和B的速度的大小;
(2)试论证小球B是否能沿着半圆轨道到达c点.
答案 (1)6.0 m/s 3.5 m/s? (2)不能
解析 (1)以v1表示小球A碰后的速度,v2表示小球B碰后的速度,v1′表示小球A在半圆最高点的速度,t表示小球A从离开半圆最高点到落在轨道上经过的时间,则有:
v1′t=4 R ①
R ①
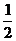 gt2=2R ②
gt2=2R ②
mg(2R)+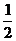 mv1′2=
mv1′2=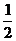 mv12 ③
mv12 ③
Mv0=mv1+Mv2 ④
由①②③④求得
v1=2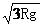 v2=v0-2
v2=v0-2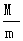
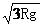
代入数值得
v1=6 m/s
v2=3.5 m/s?
(2)假定B球刚能沿着半圆的轨道上升到c点,则在c点时,轨道对它的作用力等于零,以vc表示它在c点的速度,vb表示它在b点相应的速度,由牛顿定律和机械能守恒定律,有
Mg=M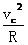
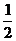 Mvc2+Mg(2R)=
Mvc2+Mg(2R)= 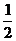 Mvb2
Mvb2
解得
vb=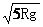
代入数值得vb=3.9 m/s?
由v2=3.5 m/s,可知v2<vb,所以小球B不能达到半圆轨道的最高点.
13.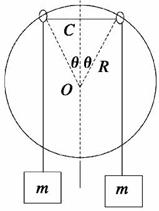 (04·江苏·15)如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,两个轻质小圆环套在大圆环上.一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小。
(04·江苏·15)如图所示,半径为R、圆心为O的大圆环固定在竖直平面内,两个轻质小圆环套在大圆环上.一根轻质长绳穿过两个小圆环,它的两端都系上质量为m的重物,忽略小圆环的大小。
⑴将两个小圆环固定在大圆环竖直对称轴的两侧 的位置上(如图).在两个小圆
的位置上(如图).在两个小圆
环间绳子的中点C处,挂上一个质量M= m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略.求重物M下降的最大距离;
m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略.求重物M下降的最大距离;
⑵若不挂重物M,小圆环可以在大圆环上自由移动,且绳子与大、小圆环及大、小圆环之间的摩擦均可以忽略.问两个小圆环分别是在哪些位置时,系统可处于平衡状态?
答案 h= R
R 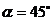
 解析 ⑴重物向下先做加速运动、后做减速运动,当重物速度为零时,下降的距离最大,设下降的最大距离为h,由机械能守恒定律得 Mgh=2mg[
解析 ⑴重物向下先做加速运动、后做减速运动,当重物速度为零时,下降的距离最大,设下降的最大距离为h,由机械能守恒定律得 Mgh=2mg[ ] 解得 h=
] 解得 h=
⑵系统处于平衡状态时,两个小环的位置为
a.两小环同时位于大圆环的底端
b.两小环同时位于大圆环的顶端
c.两小环一个位于大圆环的顶端,另一个位于大圆环的底端
d.除上述情况外,根据对称可知,系统如能平衡,则两小圆环的位置一定关于大圆环
竖直对称轴对称.设平衡时,两小圆环在大圆环竖直以对称两侧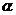 角的位置上(如图
角的位置上(如图
所示).对于重物m,受绳子拉力T与重力mg作用,有T=mg.对于小圆环,受到三个
力的作用,水平绳子的拉力T、竖直绳子的拉力T、大圆环的支持力N,两绳子的拉力沿大圆环切向分力大
小相等,方向相反T sin 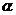 =T
sin
=T
sin 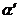 得
得 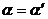 ,而,所以
,而,所以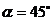 .
.
12.(04·江苏春季·13)质量M=6.0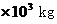 的客机,从静止开始沿平直的跑道滑行,当滑行距离:s=7.2
的客机,从静止开始沿平直的跑道滑行,当滑行距离:s=7.2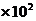 m时,达到起飞的速度v=60 m/s.
m时,达到起飞的速度v=60 m/s.
⑴起飞时飞机的动能多大?
⑵若不计滑行过程中所受的阻力,则飞机受到的牵引力为多大?
⑶若滑行过程中受到的平均阻力大小为F=3.0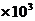 N,牵引力与第⑵问中求得的值相等,则要达到上述起飞速度,飞机的滑行距离应为多大?
N,牵引力与第⑵问中求得的值相等,则要达到上述起飞速度,飞机的滑行距离应为多大?
答案 ⑴1.08 J ⑵1.5
J ⑵1.5 N ⑶
N ⑶ m
m
解析 ⑴飞机起飞的动能为Ek=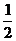 Mv2,代入数值得Ek=1.08
Mv2,代入数值得Ek=1.08 J
J
⑵设牵引力为F1,由动能定理,得F1s=Ek-0,代入数值解得F1=1.5 N
N
⑶设滑行距离为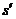 ,由动能定理,得(F1-F)
,由动能定理,得(F1-F)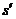 =Ek-0,整理得
=Ek-0,整理得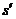 =
=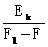 ,代入数值得
,代入数值得 m
m
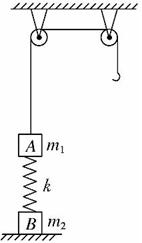
11.(05·全国卷Ⅰ·24)如图,质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连,弹簧的劲度系数为k,A、B都处于静止状态.一条不可伸长的轻绳绕过轻滑轮,一端连物体A,另一端连一轻挂钩.开始时各段绳都处于伸直状态,A上方的一段绳沿竖
直方向.现在挂钩上挂一质量为m3的物体C并从静止状态释放,已知它恰好能使B离开
地面但不继续上升.若将C换成另一个质量为(m1+m3)的物体D,仍从上述初始位置由静止状态释放,则这次B刚离地时D的速度的大小是多少?已知重力加速度为g。
答案 g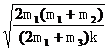
解析 解法一 开始时,A、B静止,设弹簧压缩量为x1,有
kx1=m1g ①
挂C并释放后,C向下运动,A向上运动,设B刚要离地时弹簧伸长量为x2,有
kx2=m2g ②
B不再上升表示此时A和C的速度为零,C已降到其最低点.由机械能守恒,与初始状态相比,弹簧弹性势能的增加量为ΔE=m3g(x1+x2)-m1g(x1+x2) ③
C换成D后,当B刚离地时弹簧弹性势能的增量与前一次相同,设此时A、D速度为v,由能量关系得
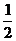 (m3+m1)v2+
(m3+m1)v2+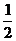 m1v2=(m3+m1)g(x1+x2)-m1g(x1+x2)-ΔE ④
m1v2=(m3+m1)g(x1+x2)-m1g(x1+x2)-ΔE ④
由①~④式得
v=g 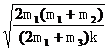
解法二 能量补偿法
据题设,弹簧的总形变量即物体A上升的距离为
h=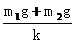 ①
①
第二次释放D与第一次释放C相比较,根据能量守恒,可得
m1gh=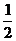 (2m1+m3)v2 ②
(2m1+m3)v2 ②
由①②得
v=g 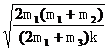
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com