
九月: 夏季风开始南撤
3、我国降水季节和年际变化大的原因
受季风气候的影响 夏季风进退规律的反常
21.[选做题]在A、B、C、D四小题中只能选做两题,每小题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
 A.选修4 - 1:几何证明选讲
A.选修4 - 1:几何证明选讲
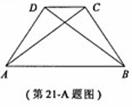
如图,在四边形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
[解析] 本小题主要考查四边形、全等三角形的有关知识,考查推理论证能力。满分10分。
证明:由△ABC≌△BAD得∠ACB=∠BDA,故A、B、C、D四点共圆,从而∠CBA=∠CDB。再由△ABC≌△BAD得∠CAB=∠DBA。因此∠DBA=∠CDB,所以AB∥CD。
B. 选修4 - 2:矩阵与变换
求矩阵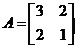 的逆矩阵.
的逆矩阵.
[解析] 本小题主要考查逆矩阵的求法,考查运算求解能力。满分10分。
解:设矩阵A的逆矩阵为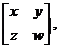 则
则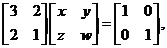
即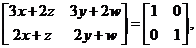 故
故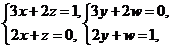
解得: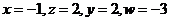 ,
,
从而A的逆矩阵为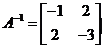 .
.
C. 选修4 - 4:坐标系与参数方程
已知曲线C的参数方程为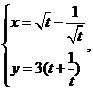 (
(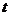 为参数,
为参数,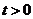 ).
).
求曲线C的普通方程。
[解析] 本小题主要考查参数方程和普通方程的基本知识,考查转化问题的能力。满分10分。
解:因为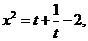 所以
所以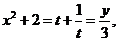
故曲线C的普通方程为: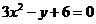 .
.
D. 选修4 - 5:不等式选讲
设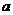 ≥
≥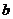 >0,求证:
>0,求证: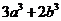 ≥
≥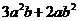 .
.
[解析] 本小题主要考查比较法证明不等式的常见方法,考查代数式的变形能力。满分10分。
证明: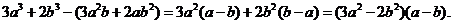
因为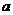 ≥
≥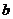 >0,所以
>0,所以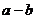 ≥0,
≥0,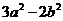 >0,从而
>0,从而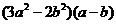 ≥0,
≥0,
即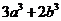 ≥
≥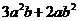 .
.
2009海南宁夏卷
(22)(本小题满分10分)选修4-1;几何证明选讲
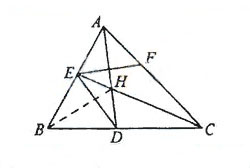
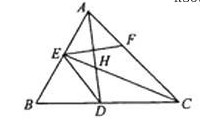 如图,已知
如图,已知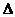 ABC中的两条角平分线
ABC中的两条角平分线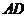 和
和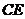 相交于
相交于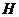 ,
,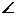 B=60
B=60 ,
,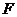 在
在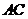 上,且
上,且 。
。
(1)证明: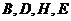 四点共圆;
四点共圆;
(2)证明:CE平分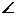 DEF。
DEF。
(22)解:
(Ⅰ)在△ABC中,因为∠B=60°,
 所以∠BAC+∠BCA=120°.
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆。
(Ⅱ)连结BH,则BH为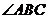 的平分线,得
的平分线,得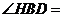 30°
30°
由(Ⅰ)知B,D,H,E四点共圆,
所以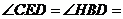 30°
30°
又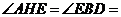 60°,由已知可得
60°,由已知可得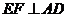 ,
,
可得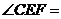 30°
30°
所以CE平分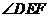
(23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C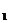 :
: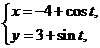 (t为参数), C
(t为参数), C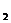 :
: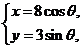 (
(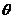 为参数)。
为参数)。
(1)化C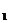 ,C
,C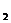 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C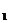 上的点P对应的参数为
上的点P对应的参数为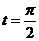 ,Q为C
,Q为C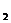 上的动点,求
上的动点,求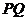 中点
中点 到直线
到直线
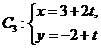 (t为参数)距离的最小值。
(t为参数)距离的最小值。
(23)解:
(Ⅰ)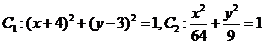
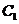 为圆心是
为圆心是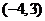 ,半径是1的圆。
,半径是1的圆。
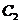 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在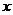 轴上,长半轴长是8,短半轴长是3的椭圆.
轴上,长半轴长是8,短半轴长是3的椭圆.
(Ⅱ)当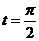 时,
时,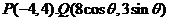 ,故
,故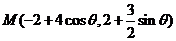
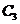 为直线
为直线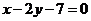 ,
,
M到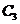 的距离
的距离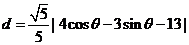
从而当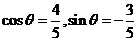 时,
时,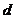 取得最小值
取得最小值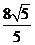
(24)(本小题满分10分)选修4-5:不等式选讲
如图,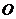 为数轴的原点,
为数轴的原点,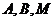 为数轴上三点,
为数轴上三点,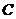 为线段
为线段 上的动点,设
上的动点,设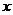 表示
表示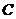 与原点的距离,
与原点的距离,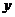 表示
表示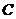 到
到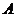 距离4倍与
距离4倍与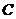 到
到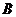 距离的6倍的和.
距离的6倍的和.
(1)将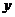 表示为
表示为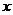 的函数;
的函数;
(2)要使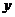 的值不超过70,
的值不超过70,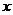 应该在什么范围内取值?
应该在什么范围内取值?

(24)解:
(Ⅰ)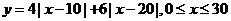
(Ⅱ)依题意,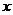 满足
满足
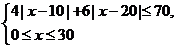
解不等式组,其解集为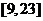
所以
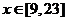
2009辽宁理卷
( 22 ) (本小题满分 10 分)选修 4- l :几何证明选讲
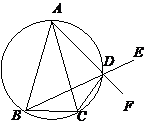 己知△ABC中,AB=AC , D是△ABC外接圆
己知△ABC中,AB=AC , D是△ABC外接圆
劣弧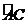 上的点(不与点A , C重合),延长BD至E。
上的点(不与点A , C重合),延长BD至E。
(1)求证:AD 的延长线平分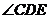 ;
;
(2)若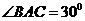 ,△ABC中BC边上的高
,△ABC中BC边上的高 ,
,
求△ABC外接圆的面积.
( 22 ) 解:( 1 )如图,设F为AD延长线上一点,∵A,B,C, D 四点共圆,
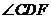 =
=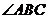 , 又AB=AC ,∴
, 又AB=AC ,∴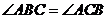 ,且
,且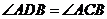 ,
,
∴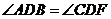 ,对顶角
,对顶角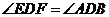 ,故
,故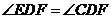 ,
,
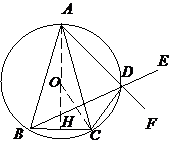 故AD 的延长线平分
故AD 的延长线平分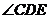 。
。
.( 2)设O为外接圆圆心,连接AO交BC于H ,则AH⊥BC ,
连接 OC ,由题意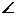 OAC=
OAC=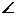 OCA =
OCA =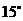 ,
,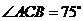 ,
,
∴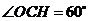 ,设圆半径为r,则
,设圆半径为r,则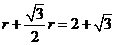 ,
,
得:r= 2 ,故外接圆面积为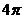 。
。
( 23 ) (本小题满分 10 分)选修 4- 4 :极坐标与参数方程
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为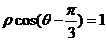 ,M , N分别为曲线C与x轴,y轴的交点.
,M , N分别为曲线C与x轴,y轴的交点.
(1)写出曲线C的直角坐标方程,并求M , N的极坐标;
(2)设M , N的中点为P,求直线OP的极坐标方程.
( 23 )解:(1)由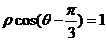 得:
得: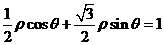 ,
,
∴曲线C的直角坐标方程为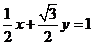 ,即
,即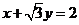 ,
,
当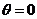 时,
时,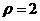 ,∴M的极坐标(2,0);
,∴M的极坐标(2,0);
当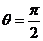 时,
时,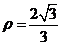 ,∴N的极坐标
,∴N的极坐标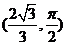 。
。
(2)M的直角坐标为(2,0),N的直角坐标为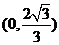 ,∴P的直角坐标为
,∴P的直角坐标为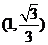 ,
,
则P的极坐标为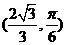 ,直线OP的极坐标方程为
,直线OP的极坐标方程为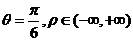 .----10分
.----10分
( 24 ) (本小题满分 10 分)选修 4- 5 :不等式选讲
设函数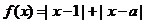 ,
,
(1)若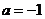 ,解不等式
,解不等式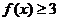 ;
;
(2)如果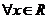 ,
,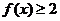 ,求a的取值范围.
,求a的取值范围.
( 24 )解:(1)当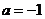 时,
时,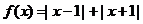 ,由
,由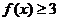 得:
得: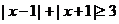 ,
,
(法一)由绝对值的几何意义知不等式的解集为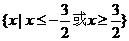 。
。
(法二)不等式可化为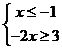 或
或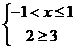 或
或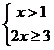 ,
,
∴不等式的解集为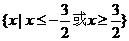 。
。
(2)若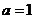 ,
,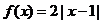 ,不满足题设条件;
,不满足题设条件;
若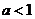 ,
,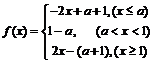 ,
,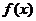 的最小值为
的最小值为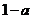 ;
;
若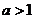 ,
,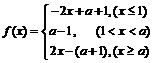 ,
,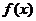 的最小值为
的最小值为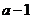 。
。
所以对于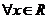 ,
,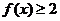 的充要条件是
的充要条件是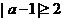 ,从而a的取值范围
,从而a的取值范围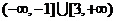 。
。
15.(几何证明选讲选做题)如图4,点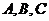 是圆
是圆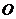 上的点, 且
上的点, 且 , 则圆
, 则圆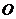 的面积等于
.
的面积等于
.
[解析]解法一:连结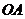 、
、 ,则
,则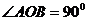 ,∵
,∵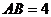 ,
,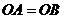 ,∴
,∴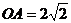 ,则
,则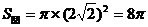 ;解法二:
;解法二: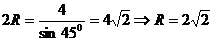 ,则
,则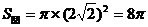 .
.
2009江苏卷
14.(不等式选讲选做题)不等式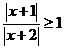 的实数解为 .
的实数解为 .
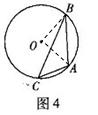 [解析]
[解析]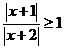
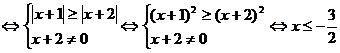 且
且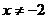 .
.
13.(坐标系与参数方程选做题)若直线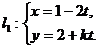 (
(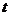 为参数)与直线
为参数)与直线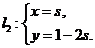 (
(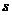 为参数)垂直,则
为参数)垂直,则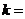 .
.
[解析]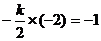 ,得
,得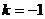 .
.
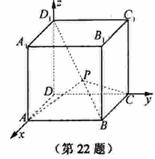
22.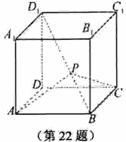 [必做题]如图,设动点P是棱长为1的正方体
[必做题]如图,设动点P是棱长为1的正方体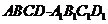 的对角线
的对角线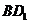 上一点,记
上一点,记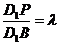 .当
.当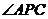 为钝角时,求
为钝角时,求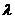 的取值范围.
的取值范围.
解:由题设可知,以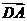 、
、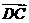 、
、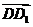 为单位正交基底,建立如图所示的空间直角坐标系
为单位正交基底,建立如图所示的空间直角坐标系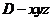 ,
,
则有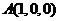 ,
,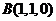 ,
, ,
,
由 ,得
,得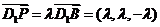 ,
,
所以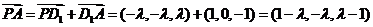
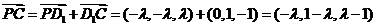
显然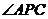 不是平角,所以
不是平角,所以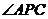 为钝角等价于
为钝角等价于
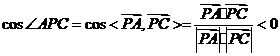 ,则等价于
,则等价于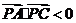 ,
,
即 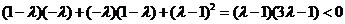 ,得
,得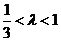 .
.
因此,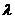 的取值范围是
的取值范围是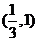
22、(本小题满分10分)选修4-1:几何证明选讲
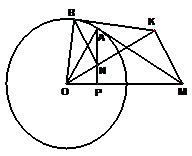 如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P。
如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P。
(Ⅰ)证明:OM·OP = OA2;
(Ⅱ)N为线段AP上一点,直线NB垂直直线ON,且交
圆O于B点。过B点的切线交直线ON于K。证明:∠OKM = 90°。
[试题解析]:(Ⅰ)证明:因为MA是圆O的切线,所以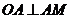 .
.
又因为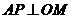 ,在
,在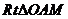 中,由射影定理知,
中,由射影定理知,
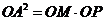 .
.
(Ⅱ)证明:因为BK是圆O的切线, 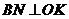 ,
,
同(Ⅰ),有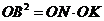 ,
, 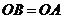 .
.
所以 ,即
,即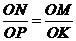 .
.
又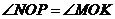 ,
,
所以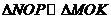 ,故
,故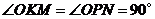 .
.
[高考考点]圆的有关知识及应用
[易错点]:对有关知识掌握不到位而出错
[备考提示]:高考对平面几何的考查一直要求不高,故要重点掌握,它是我们的得分点之一。
(23)(本小题满分10分)选修4-4;坐标系与参数方程
已知曲线C1: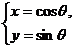 (
(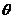 为参数),曲线C2:
为参数),曲线C2: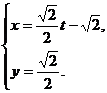 (t为参数)。
(t为参数)。
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线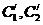 。写出
。写出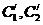 的参数方程。
的参数方程。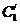 与
与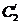 公共点的个数和C
公共点的个数和C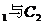 公共点的个数是否相同?说明你的理由。
公共点的个数是否相同?说明你的理由。
[试题解析]:(Ⅰ)C1是圆,C2是直线,
C1的普通方程是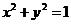 ,C2的普通方程是
,C2的普通方程是 .
.
因为圆心C1到直线 的距离是1,
的距离是1,
所以C1与C2只有一个公共点.
(Ⅱ)压缩后的参数方程分别为C1: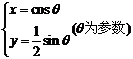 ,
,
曲线C2: .
.
化为普通方程为 :
: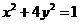 ,
,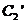 :
: 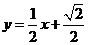 .
.
联立消元得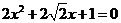 ,
,
其判别式 ,
,
所以压缩后的直线 与椭圆
与椭圆 仍然只有一个公共点,和C1与C2的公共点的个数相同。
仍然只有一个公共点,和C1与C2的公共点的个数相同。
[高考考点]参数方程与普通方程的互化及应用
[易错点]:对有关公式掌握不到位而出错.
 [备考提示]:高考对参数方程的考查要求也不高,故要重点掌握,它也是我们的得分点之一
[备考提示]:高考对参数方程的考查要求也不高,故要重点掌握,它也是我们的得分点之一
(24)(本小题满分10分)选修4-5:不等式选讲
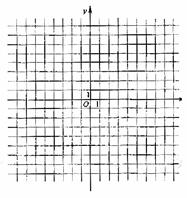
已知函数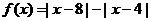 。
。
(Ⅰ)作出函数 的图像;
的图像;
(Ⅱ)解不等式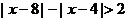 。
。
[试题解析]:(Ⅰ)令 ,则
,则
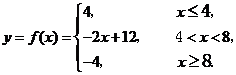 ...............3分
...............3分
图象如图所示,
(Ⅱ)不等式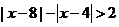 ,即
,即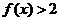 .
.
由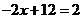 得
得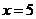 .
.
由函数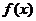 图象可知,原不等式的解集为
图象可知,原不等式的解集为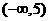 .
.
[高考考点]绝对值不等式的有关知识及应用本题主要考查参数方程与普通方程的互化,以及转化与化归的思想,分析问题与解决问题的能力。
[易错点]:对绝对值不等式不会灵活分类而出错.
[备考提示]:高考对绝对值不等式的考查要求不高,以中档题为主,故是我们的得分点之一,平时复习时不要盲目加深。
(2008江苏卷)附加题
21:从A,B,C,D四个中只能选做2题,每小题10分,共计20分。
A.选修4-1:几何证明选讲
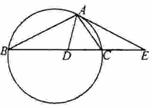 如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.求证:
如图,设△ABC的外接圆的切线AE与BC的延长线交于点E,∠BAC的平分线与BC交于点D.求证: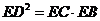 .
.
证明:如图,因为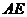 是圆的切线,
是圆的切线,
所以,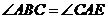 ,
,
又因为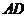 是
是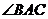 的平分线,
的平分线,
所以 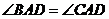
从而 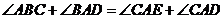
因为 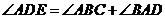 ,
,

所以 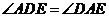 ,故
,故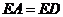 .
.
因为 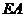 是圆的切线,所以由切割线定理知,
是圆的切线,所以由切割线定理知,
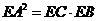 ,
,
而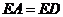 ,所以
,所以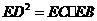 。
。
B.选修4-2 矩阵与变换
在平面直角坐标系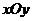 中,设椭圆
中,设椭圆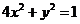 在矩阵
在矩阵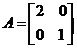 对应的变换作用下得到曲线F,求F的方程.
对应的变换作用下得到曲线F,求F的方程.
解:设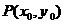 是椭圆上任意一点,点
是椭圆上任意一点,点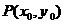 在矩阵
在矩阵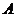 对应的变换下变为点
对应的变换下变为点
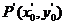 则有
则有
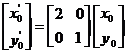 ,即
,即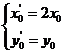 ,所以
,所以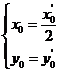
又因为点 在椭圆上,故
在椭圆上,故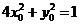 ,从而
,从而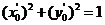
所以,曲线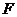 的方程是
的方程是 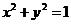
C.选修4-4 参数方程与极坐标
在平面直角坐标系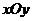 中,点
中,点 是椭圆
是椭圆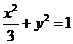 上的一个动点,求
上的一个动点,求 的最大值.
的最大值.
解: 因椭圆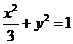 的参数方程为
的参数方程为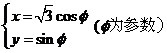
故可设动点 的坐标为
的坐标为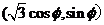 ,其中
,其中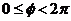 .
.
因此
所以,当 时,
时,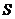 取得最大值2。
取得最大值2。
D.选修4-5 不等式证明选讲
设a,b,c为正实数,求证: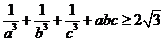 .
.
证明:因为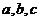 为正实数,由平均不等式可得
为正实数,由平均不等式可得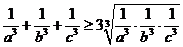
即
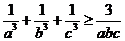
所以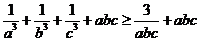 ,
,
而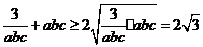
所以 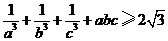 。
。
15.(几何证明选讲选做题)已知PA是圆O的切点,切点为A,PA=2.AC是圆O的直径,PC与圆O交于B点,PB=1,则圆O的半径R=________.
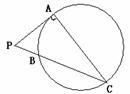 [解析]依题意,我们知道
[解析]依题意,我们知道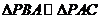 ,由相似三角形的性质我们有
,由相似三角形的性质我们有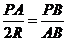 ,即
,即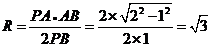 。
。

(2008海南、宁夏)
14.(坐标系与参数方程选做题)已知曲线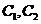 的极坐标方程分别为
的极坐标方程分别为
 ,则曲线
,则曲线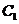
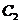 交点的极坐标为
。
交点的极坐标为
。
[解析]我们通过联立解方程组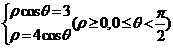 解得
解得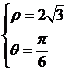 ,即两曲线的交点为
,即两曲线的交点为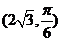 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com