
2、一个反比例函数的图像经过点P(-1,5),则这个函数的表达式是___________________
1、-5的倒数是______________
3、如图,在△ABC中,AB=BC=5,BC=8, 点E、F是中线AD上的两点,则图中阴影部份面积为( )
A.10 B.20 C.30 D.40
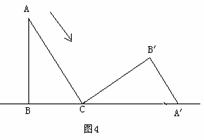 4、如图,一块含有30°的直角三角板ABC在水平桌面上绕点C按顺时针方向旋转到
4、如图,一块含有30°的直角三角板ABC在水平桌面上绕点C按顺时针方向旋转到
A′B′C′位置。若BC边长为15㎝,那么顶点A从开始到结束所经过的路径长为( )
A.10л㎝ B.10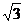 л㎝ C.15л㎝
D.20л㎝
л㎝ C.15л㎝
D.20л㎝
1、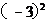 -
-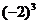 的结果是(
)
的结果是(
)
A. -1 B.1 C. -17 D.17
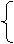 2、不等式组 2x-1≤3
2、不等式组 2x-1≤3
X>-1 的结果是 ( )
 A.x<2
B. x>1
C.x≤2
D. -1<x≤2
A.x<2
B. x>1
C.x≤2
D. -1<x≤2
1.下列计算中,正确的是 ( )
 A.
A.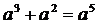 B.
B.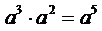
C.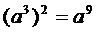 D.
D.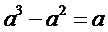
[命题意图]在选择题、填空题中突出考查对基础知识的理解和运用,本题主要考察有理数的运算,十分简单.
19. 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 为直径的圆.
为直径的圆.
 (1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
 (3)某地有四个村庄
(3)某地有四个村庄 (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
[命题意图]考查学生尺规作图,圆的基础知识
[参考答案]解:(1)如图所示: 4分
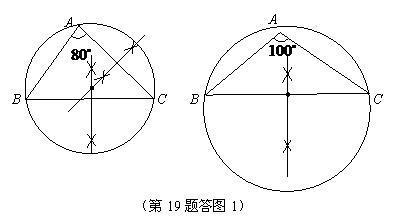
(注:正确画出1个图得2分,无作图痕迹或痕迹不正确不得分)
(2)若三角形为锐角三角形,则其最小覆盖圆为其外接圆; 6分
若三角形为直角或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆. 8分
 (3)此中转站应建在
(3)此中转站应建在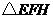 的外接圆圆心处(线段
的外接圆圆心处(线段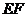 的垂直平分线与线段
的垂直平分线与线段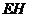 的垂直平分线的交点处).·················· 10分
的垂直平分线的交点处).·················· 10分
理由如下:
由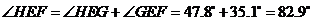 ,
,
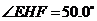 ,
,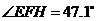 ,
,
故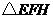 是锐角三角形,
是锐角三角形,
所以其最小覆盖圆为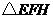 的外接圆,
的外接圆,
设此外接圆为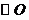 ,直线
,直线 与
与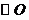 交于点
交于点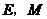 ,
,
则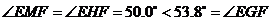 .
.
故点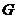 在
在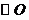 内,从而
内,从而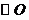 也是四边形
也是四边形 的最小覆盖圆.
的最小覆盖圆.
所以中转站建在 的外接圆圆心处,能够符合题中要求.
的外接圆圆心处,能够符合题中要求.
····················· 12分
[试题来源]2008年连云港中考试题
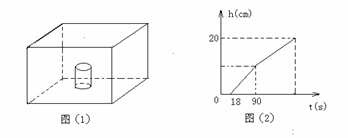
18.在底面积为100cm2、高为20cm2的长方体水槽内放入一个圆柱形烧杯(烧杯本身的质量、体积忽略不计),如图(1)所示,向烧杯中注入流量一定的水,注满烧杯后,继续注水,直至注满水槽为止,(烧杯在水槽中的位置始终不变),水槽中水面上升的高度h与注水时间t之间的函数关系如图(2)所示。
(1)求烧杯的底面积;(6)分
(2)若烧杯的高为9cm,求注水的速度及注满水槽所用时间(6)分
[命题意图]由函数变化关系研究事件变化情况及准确的得关系式
[参考答案]设烧杯的底面积为Scm2、高为h1cm,注水速度为v cm3/s,注满水槽所用时间为t0s.
(1)由图2知,当注水18s时,烧杯刚好注满;当注水90s时,水槽内的水面高度恰好是h1cm(即烧杯高度)。于是,
Sh1=18 v,100h1=90v
则有100h1=90×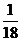 sh1,即S=20
sh1,即S=20
所以,烧杯的底面积为20cm2 (6)分
(2)若h1=9,则
v=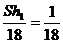 ×20×9=10
×20×9=10
所以,注水速度为10cm3/s
由vt0=100×20,解得t0=200
因此,注满水槽所用时间为200s (6)分
[试题来源]德清县初中数学通讯赛
17. 如图,已知直线l:y=kx+2,k<0 ,与y轴交于点A,与x轴交于点B,以OA为直径的⊙P交l于另一点D,把弧AD沿直线l翻转后与OA交于点E。
(1)当k=-2时,求OE的长(4)分
(2)是否存在实数k,k<0 ,使沿直线l把弧AD翻转后所得的弧与OA相切?
若存在,请求出此时k的值,若不存在,请说明理由。(6)分
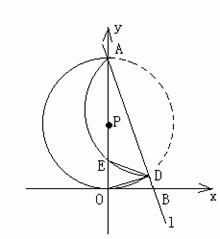
[命题意图]圆在坐标系的变换情况
[参考答案]答案:如图所示,由
∠DEO=∠EAD+∠ADE=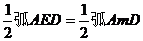
=∠AOD
所以,OD=DE
当k=-2时,易得A(0,2),B(1,0),OA=2,OB=1,则AB=
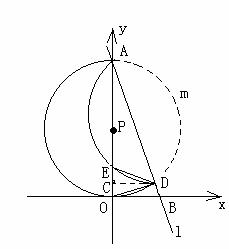 因为BO与⊙P切于点O,由切割线定理,得
因为BO与⊙P切于点O,由切割线定理,得
OB2=BD·AB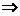 BD=
BD=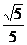
过点D作DC⊥AO于点C,则
OE=2OC,DC∥OB
从而,有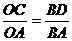
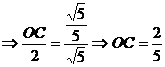
故OE=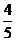 (4)
(4)
(2)假设存在实数k使得弧AD沿直线l翻转后所得弧与OA相切,则切点必为A,即E与A重合,由(1)知OD=AD。
又∠ADO=90°,所以
∠OAD=45°
此时,OB=OA=2,B(2,0)
∴k=-1,
故存在k=-1,使得弧AD沿直l翻转后所得弧与OA相切。 (6)
[试题来源]2009北京中考模拟
16. 已知关于x的一元二次方程 (6-k)(9-k)x2-(117-15k)x+54=0的两个根均为整数,求所有满足条件的实数k的值。(本题满分10分)
[命题意图]一元二次方程根与系数关系
[参考答案]解:原方程可化为
[(6-k)x-9][(9-k)x-6]=0
因为此方程是关于x的一元二次方程,所以,k≠6,k≠9,于是,有
x1=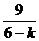 ,x2=
,x2= (5)分
(5)分
消去k,得x1x2-2x1+3x2=0,有
(x1+3)(x2-2)=-6
因为x1、x2均为整数,所有,

故x1=-9,-6,-5,-4,-2,-1,0,3 (5)分
又k=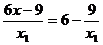 ,将x1=-9,-6,-5,-4,-2,-1,3分别代入,得
,将x1=-9,-6,-5,-4,-2,-1,3分别代入,得
k=7,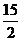 ,
,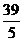 ,
, ,
,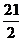 ,15,3
(10)分
,15,3
(10)分
[试题来源]本校月考加工总结所得
15. (本题满分10分) 如图10,一次函数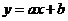 的图象与反比例函数
的图象与反比例函数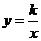 的图象交于M、N两点.
的图象交于M、N两点.
(1)求反比例函数和一次函数的解析式;
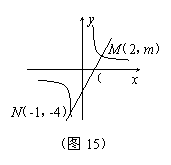 (2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
(2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
[命题意图]一次函数和反比例函数的综合应用
[参考答案](1)将N(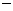 1,
1,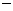 4)代入
4)代入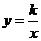 中 得k=4
(2分)
中 得k=4
(2分)
反比例函数的解析式为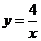 (3分)
(3分)
将M(2,m)代入解析式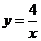 中 得m=2
(4分)
中 得m=2
(4分)
将M(2,2),N(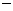 1,
1,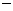 4)代入
4)代入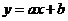 中
中
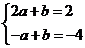 解得a=2 b=-2
(5分)
解得a=2 b=-2
(5分)
一次函数的解析式为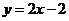 (6分)
(6分)
[试题来源]本校月考加工总结所得
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com