
1.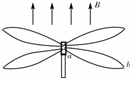 (05年如东)一直升飞机停在南半球某处上空.设该处地磁场的方向竖直向上,磁感应强度为B.直升飞机螺旋桨叶片的长度为l,螺旋桨转动的频率为f,顺着地磁场的方向看螺旋桨,螺旋桨按顺时针方向转动.螺旋桨叶片的近轴端为a,远轴端为b,如图所示.如果忽略到转轴中心线的距离,用E表示每个叶片中的感应电动势,则 ( A )
(05年如东)一直升飞机停在南半球某处上空.设该处地磁场的方向竖直向上,磁感应强度为B.直升飞机螺旋桨叶片的长度为l,螺旋桨转动的频率为f,顺着地磁场的方向看螺旋桨,螺旋桨按顺时针方向转动.螺旋桨叶片的近轴端为a,远轴端为b,如图所示.如果忽略到转轴中心线的距离,用E表示每个叶片中的感应电动势,则 ( A )
A.E = πfl2B,且a点电势低于b点电势
B.E = 2πfl2B,且a点电势低于b点电势
C.E = πfl2B,且a点电势高于b点电势
D.E = 2πfl2B,且a点电势高于b点电势
2.应用法拉第电磁感应定律时应注意:
①一般用E = n(或E = )求平均电动势,用E = Blυ求瞬时电动势,但当Δs随Δt均匀变化时,由于电动势恒定,平均电动势和瞬时电动势相等,可用E = n求某一时刻的电动势;
②匀强磁场中,B、l、υ相互垂直,导体平动切割磁感线时E = Blυ,绕固定转轴转动时E = Bl2ω.
规律方法
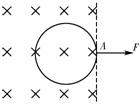 [例1]如图所示,在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,有一个质量为m、半径为r、电阻为R的均匀圆形导线圈,线圈平面跟磁场垂直(位于纸面内),线圈与磁场边缘(图中虚线)相切,切点为A,现在A点对线圈施加一个方向与磁场垂直,位于线圈平面内的,并跟磁场边界垂直的拉力F,将线圈以速度υ匀速拉出磁场.以切点为坐标原点,以F的方向为正方向建立x轴,设拉出过程中某时刻线圈上的A点的坐标为x.
[例1]如图所示,在磁感应强度大小为B,方向垂直纸面向里的匀强磁场中,有一个质量为m、半径为r、电阻为R的均匀圆形导线圈,线圈平面跟磁场垂直(位于纸面内),线圈与磁场边缘(图中虚线)相切,切点为A,现在A点对线圈施加一个方向与磁场垂直,位于线圈平面内的,并跟磁场边界垂直的拉力F,将线圈以速度υ匀速拉出磁场.以切点为坐标原点,以F的方向为正方向建立x轴,设拉出过程中某时刻线圈上的A点的坐标为x.
(1)写出此时F的大小与x的关系式;
(2)在F-x图中定性画出F-x关系图线,写出最大值F0的表达式.
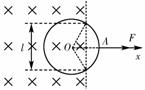 [解析]由于线圈沿F方向作切割磁感线运动,线圈上要产生顺时针方向的感应电流,从而要受到与F方向反向的安培力Ff作用,由图可知,此时线圈切割磁感线的有效长度l = 2
[解析]由于线圈沿F方向作切割磁感线运动,线圈上要产生顺时针方向的感应电流,从而要受到与F方向反向的安培力Ff作用,由图可知,此时线圈切割磁感线的有效长度l = 2
线圈上感应电动势,感应电流i =
线圈所受安培力大小为Ff = Bil,方向沿x负方向
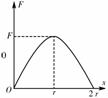 因线圈被匀速拉出,所以F = Ff
因线圈被匀速拉出,所以F = Ff
解上各式得F = x-x2
(2)当x = r时,拉力F最大,最大值为F0 =
图线如图所示.
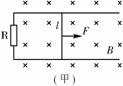
训练题如图(甲)所示,一对平行光滑轨道放置在水平面上,两轨道间距l=0.20m,电阻R=1.0Ω;有一导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻皆可忽略不计,整个装置处于磁感强度B=0.50T的匀强磁场中,磁场方向垂直轨道面向下,现用一外力F沿轨道方向拉杆,使之做匀加速运动,测得力F与时间t的关系如图(乙)所示,求杆的质量m和加速度a.
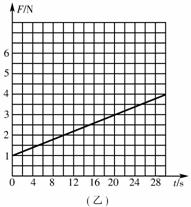 答案:a=10m/s2,m=0.1kg
答案:a=10m/s2,m=0.1kg
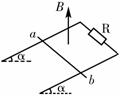 [例2]如图所示,两根相距l平行放置的光滑导电轨道,与水平面倾角均为α轨道间有电阻R,处于磁感应强度为B方向竖直向上的匀强磁场中,一根质量为m、电阻为R/4的金属杆ab,由静止开始沿导电轨道下滑.设下滑中ab杆始终与轨道保持垂直,且接触良好,导电轨道有足够的长度,且电阻不计,求ab杆沿轨道下滑可达到的最终速度.
[例2]如图所示,两根相距l平行放置的光滑导电轨道,与水平面倾角均为α轨道间有电阻R,处于磁感应强度为B方向竖直向上的匀强磁场中,一根质量为m、电阻为R/4的金属杆ab,由静止开始沿导电轨道下滑.设下滑中ab杆始终与轨道保持垂直,且接触良好,导电轨道有足够的长度,且电阻不计,求ab杆沿轨道下滑可达到的最终速度.
[解析]当ab杆沿轨道加速下滑至速度υ时,ab杆上的电动势为E = BLυcosα
ab杆与导电轨道组成的回路中的电流为I = 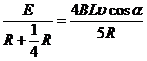
ab杆受到的安培力为F = BIl = 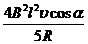 方向水平向右.
方向水平向右.
当ab杆的速度增大至某一值υm时,ab杆受到的合外力F合恰减为零,此时ab杆的加速度a也减为零,之后ab杆保持速度υm沿轨道匀速下滑.速度υm即是ab杆沿轨道下滑可达到的最终速度.
据共点合力平衡条件,有mgsinα = Fcosα
即mgsinα
=  ·cosα,解得:υm =
·cosα,解得:υm = 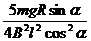 .
.
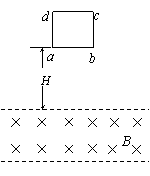 训练题如图所示,具有水平的上界面的匀强磁场,磁感强度为B,方向水平指向纸内,一个质量为m,总电阻为R的闭合矩形线框abcd在竖直平面内,其ab边长为L,bc边长为h,磁场宽度大于h,线框从ab边距磁场上界面H高处自由落下,线框下落时,保持ab边水平且线框平面竖直.已知ab边进入磁场以后,cd边到达上边界之前的某一时刻线框的速度已达到这一阶段的最大值,此时cd边距上边界为h1,求:
训练题如图所示,具有水平的上界面的匀强磁场,磁感强度为B,方向水平指向纸内,一个质量为m,总电阻为R的闭合矩形线框abcd在竖直平面内,其ab边长为L,bc边长为h,磁场宽度大于h,线框从ab边距磁场上界面H高处自由落下,线框下落时,保持ab边水平且线框平面竖直.已知ab边进入磁场以后,cd边到达上边界之前的某一时刻线框的速度已达到这一阶段的最大值,此时cd边距上边界为h1,求:
(1)线框ab边进入磁场时的速度大小;
(2)从线框ab边进入磁场到线框速度达到最大的过程中,线框中产生的热量;
答案:(1)v=(2gh)1/2
(2)Q=mg(H+h+h1)-m3R2g2/2B4L4
能力训练
1.楞次定律:
推广可以具体简化为以下三种情况:①阻碍原磁通的变化;②阻碍导体间的相对运动;③阻碍原电流的变化.
18.如图,在Rt△ABC中,∠C=90°,AC=12,BC=16,动点P从点A出发沿AC边向点C以每秒3个单位长的速度运动,动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动.P,Q分别从点A,C同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ关于直线PQ对称的图形是△PDQ.设运动时间为t(秒).
(1)设四边形PCQD的面积为y,求y与t的函数关系式;
 (2)t为何值时,四边形PQBA是梯形?
(2)t为何值时,四边形PQBA是梯形?
(3)是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,
请说明理由;
(4)通过观察、画图或折纸等方法,猜想是否存在时刻t,使得PD⊥AB?
若存在,请估计t的值在括号中的哪个时间段内(0≤t≤1;1<t≤2;
2<t≤3;3<t≤4);若不存在,请简要说明理由
[命题意图]最后总是函数的应用,去年是一次函数的应用、二次函数的应用以及分类讨论,其实对初中而言,一次函数和二次函数的重要性是一样的,关键是函数思想的确立,函数模型的建立。本题考查求解二次函数关系式、并利用关系式求值的运算技能和从情景中提取信息、解释信息、解决问题的能力,同时考查的数学思想主要是数学建模思想。本题在呈现方式上做出了创新,试题贴近社会经济的盈亏问题,赋予了生活气息,使学生真切地感受到“数学来源于生活”,体验到数学的“有用性”。 这样设计体现了《新课程标准》的“问题情景-建立模型-解释、应用和拓展”的数学学习模式。
[参考答案](1)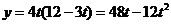
(2)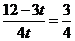
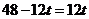
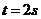
(3)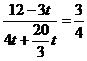
48-12t=12t+20t
48=44t
t= s
s
(4)存在时刻t使得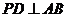 ,在时间t时
,在时间t时
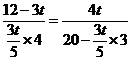 ,
,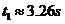 ,
,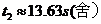
也是就说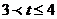
答:略
16.如图,A、B是两个蓄水池,都在河流的同旁,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两池,问该站建在河边哪一点,可使所修的渠道最短,试在图中画出该点(不写作法,但国保留作图痕迹)
。B
。A

[命题意图]本题是学生非常熟悉的“直线上一点到两点距离和”问题,来源于课本(八年级上册74页B组第1题:要在高压输电线的旁边修一个小型变电站,问该变电站建在输电线旁边什么地方,才能使变电站到A村和B村架设的电线线路最短)。对于本题情景学生非常熟悉,但它不是教材上内容的简单搬移,而是解决了同一类问题的一般情况。求稳定的同时,又有一些情景新颖、立意新颖本题给学生展现了“从问题的提出、方案设计、特殊赋值、归纳提升、问题解决”的课题学习的完整过程,以课题学习形式考查是一种新的有益尝试。
评试题的特色和亮点:将轴对称应用于当前的社会实际问题中。
试题测试后的讲评意见:加强对作图问题的理解。虽不写作法,但要注意作图步骤。
[参考答案]略
[试题来源]自编、改编
15.每年的3-10月份为一年中的黄金旅游月份。灌云县伊山镇水果种植大户田致富,为了吸引更多的顾客,组织了观光采摘游活动.每一位来采摘水果的顾客都有一次抽奖机会:在一只不透明的盒子里有 四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
(1)请利用树状图(或列表)的方法,表示前后两次抽得的卡片所有可能的情况;
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?




A B C D
[命题意图]把现实生活中学生熟悉的一些“资源”作为命题的素材,这样的试题不仅使学生感到亲切,而且有助于学生在解决问题的过程中感受数学的价值,有利于引导学生关注社会,关注数学与生活的联系,体现从生活走向数学,从数学走向社会的课程理念。
评试题的特色和亮点:将概率的知识应用与当前的社会实际问题中。
试题测试后的讲评意见:加强对题目含义的理解。问题较简单,容易解决。
[参考答案](1)4(2)1/2
[试题来源]自编、改编
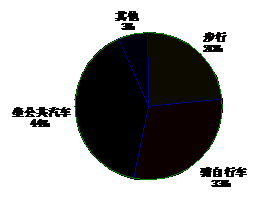
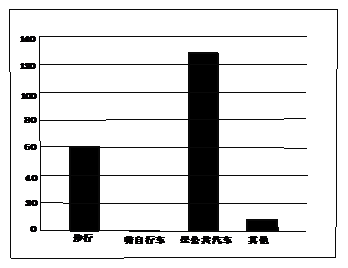
14.灌云县某中学在危房改造后准备搬迁新校舍,在迁入新校舍之前,同学们就该校学生如何到校问题进行了一次调查,并将调查结果制成了表格、条形图和扇形统计图,请你根据图表信息完成下列各题:
|
步行 |
骑自行车 |
坐公共汽车 |
其他 |
|
60 |
|
|
|
(1)此次共调查了多少位学生?
(2)请将表格填充完整;
(3)请将条形统计图补充完整.
[命题意图]本题利用两种统计图的各自的特点,使信息在两种统计图之间交叉呈现,较好地考查了从统计图中获取信息的能力,绘图的技能,以耳目一新的感觉,实现常考常新,不落俗套并将统计问题与概率进行了有机整合,统计教学既要有统计量的计算,更要有对统计结果的合理解释与正确运用,这是新课标对统计内容所赋予的新的定位,也是统计学科本身的特点所决定的。种子发芽试验,能抽象到课标所要求的“能根据统计结果作出合理的判断和预测,体会统计对决策的作用,能比较清晰地表达自己的观点”
本试题突出考查学生在学习数学和运用数学解决问题过程中最为重要的也是必须掌握的核心观念、思想方法、基本概念和常用技能。强化对数学通性通法的考查。
评试题的特色和亮点:将统计的知识应用与当前的学校实际问题中。
试题测试后的讲评意见:加强对语言叙述含义的理解。
[参考答案](1)300人(2)
|
步行 |
骑自行车 |
坐公共汽车 |
其他 |
|
60 |
99 |
132 |
9 |
(3)略。
[试题来源]自编、改编
13.
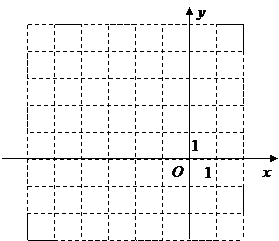 已知⊙O1经过
已知⊙O1经过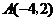 ,
,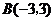 ,
,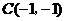 ,
,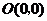 四点,一次函数
四点,一次函数 的图象是直线
的图象是直线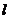 ,直线
,直线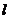 与
与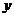 轴交于点
轴交于点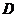 .
.
(1)在右边的平面直角坐标系中画出⊙O1,直线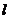 与⊙O1的交点坐标为
;
与⊙O1的交点坐标为
;
(2)若⊙O1上存在整点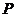 (横坐标与纵坐标均为整数的点称为整点),使得
(横坐标与纵坐标均为整数的点称为整点),使得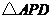 为等腰三角形,所有满足条件的点
为等腰三角形,所有满足条件的点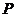 坐标为
;
坐标为
;
(3)将⊙O1沿 轴向右平移
个单位时,⊙O1与
轴向右平移
个单位时,⊙O1与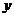 相切.
相切.
(4)将⊙O1沿 轴向右平移
个单位时,⊙O1与
轴向右平移
个单位时,⊙O1与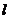 相切
相切
[命题意图]以网格作为载体,将圆的直观性见于图形的直观性基础之上,考查了圆的切线概念与性质。这是一道典型的现在常出的问题。在去年的最后一次期末考试中已经见到。加强对这类问题的理解和掌握。
试题的特色和亮点:将圆的性质置于连云港最流行的网格中。
试题测试后的讲评意见:利用网格图的直观性,加强动手操作。
[参考答案](1)(-4,2)(-1,-1)(2)(0,2)(-3,-1)(3)2+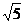 。
。
(4)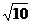 -1
-1
[试题来源]自编、改编
12.如图,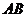 是⊙O的直径,
是⊙O的直径, 切⊙O于
切⊙O于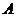 ,
,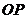 交⊙O于
交⊙O于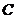 ,连
,连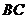 .若
.若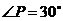 ,求
,求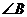 的度数.
的度数.


[命题意图]这是一道应用圆切线的性质以及三角形外角的性质来建立的问题,这样的求稳定的同时,又有一些情景新颖
考法常常能更好地考查学生的基础意识,以及简单的运用方程思想解决问题的能力。
试题的特色和亮点:能直接利用性质进行必要的计算,属于中考容易得分的题目。
试题测试后的讲评意见:复习切线的性质,掌握思考的方法。
[参考答案]300。
[试题来源]自编
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com