
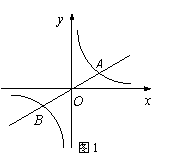
5、(2007浙江金华)如图1,已知双曲线y=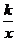 (k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;
(k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;
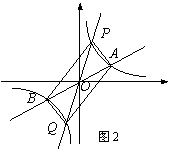
(2)如图2,过原点O作另一条直线l,交双曲线y=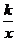 (k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行四边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出mn应满足的条件;若不可能,请说明理由.
(k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行四边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出mn应满足的条件;若不可能,请说明理由.


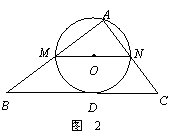
4.(08山东省日照市)在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?


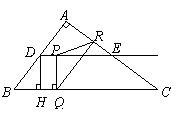
3. (08浙江温州)如图,在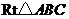 中,
中,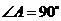 ,
,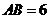 ,
,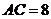 ,
,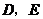 分别是边
分别是边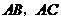 的中点,点
的中点,点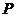 从点
从点 出发沿
出发沿 方向运动,过点
方向运动,过点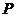 作
作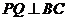 于
于 ,过点
,过点 作
作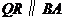 交
交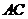 于
于
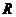 ,当点
,当点 与点
与点 重合时,点
重合时,点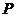 停止运动.设
停止运动.设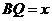 ,
,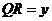 .
.
(1)求点 到
到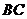 的距离
的距离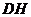 的长;
的长;
(2)求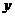 关于
关于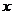 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点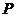 ,使
,使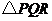 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的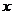 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
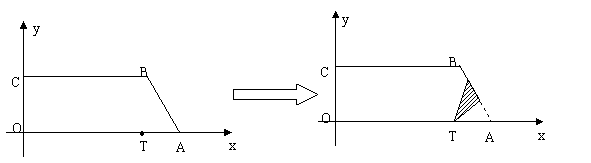
2. (08浙江衢州)已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,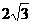 ),C(0,
),C(0,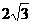 ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;
(2)当纸片重叠部分的图形是四边形时,求t的取值范围;
(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由.
1.(2008年四川省宜宾市)
已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
(1) 求该抛物线的解析式;
(2) 若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;
(3) △AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为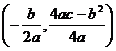 )
)

.
4.(1)当点P在BA上运动时,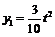 ;
;
当点P在AD上运动时,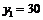 ;
;
当点P在DC上运动时,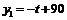
(2)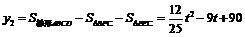 ,自变量
,自变量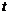 的取值范围是0≤
的取值范围是0≤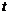 ≤5.
≤5.
本资料由《七彩教育网》 提供!
3.(1)2秒或4秒
(2)存在点P、Q,使得△PBQ的面积等于9㎝2,有两种情况:
①点P在AB边上距离A为3㎝,点Q在BC边上距离点B为6㎝;
②点P在BC边上,距B点3㎝时,此时Q点就是A点
2.(1)C(1,2)
(2)-10≤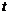 ≤2
≤2
(3)S与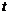 的函数关系式为
的函数关系式为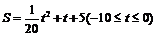 或
或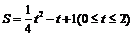
1.A
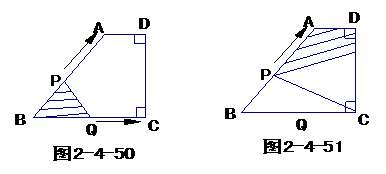
4.如图2-4-49,在梯形ABCD中,AB=BC=10㎝,CD=6㎝,∠C=∠D=900.
(1)如图2-4-50,动点P、Q同时以每秒1㎝的速度从点B出发,点P沿BA、AD、DC运动到点C停止.设P、Q同时从点B出发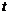 秒时,△PBQ的面积为
秒时,△PBQ的面积为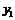 (㎝2),求
(㎝2),求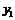 (㎝2)关于
(㎝2)关于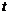 (秒)的函数关系式.
(秒)的函数关系式.
(2)如图2-4-51,动点P以每秒1㎝的速度从点B出发沿BA运动,点E在线段CD上随之运动,且PC=PE.设点P从点B出发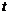 秒时,四边形PADE的面积为
秒时,四边形PADE的面积为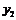 (㎝2).求
(㎝2).求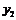 (㎝2)关于
(㎝2)关于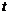 (秒)的函数关系式,并写出自变量
(秒)的函数关系式,并写出自变量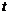 的取值范围.
的取值范围.
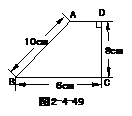
[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com