
1、在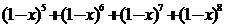 的展开式中,含
的展开式中,含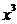 的项的系数是(D
)
的项的系数是(D
)
A.74 B.121 C.-74 D.-121
22.解法一:(1)取BC的中点H,连EH,易得EH是EF在平面AC上的射影,
∵BD⊥EH,∴由三垂线定理,得 EF⊥BD;
又∵EF在平面AB1上的射影是B1E,由△BB1E∽△ABG,得B1E⊥BG,∴由三垂线定理,得 EF⊥BG,
∵BG∩BD=B,∵EF⊥平面GBD.
(2)取C1D1的中点M,连EM,易得EM∥AD1,所以∠EFM就是异面直线AD1与EF所成的角,
∵MF∥BD,∴EF⊥MF .在Rt△EFM中,由EM=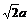 ,(a为正方体的棱长),EF=
,(a为正方体的棱长),EF= ,得
,得
∠EFM=30º.即异面直线AD1与EF所成的角为30º.
解法二:(向量法)(1) 以AD为x轴,DC为y轴,DD1为z轴建立空间坐标系,不妨设正方体的棱长为2,
则D(0,0,0),A(2,0,0),B(2,2,0),E(2,1,0),F(1,2,2),G(2,,0,1) ,D1(0,0,2 )
∵ (2,2,0)·(1,-1,-2)=0,
(2,2,0)·(1,-1,-2)=0,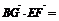 (0,-2,1)·(1,-1,-2)=0
(0,-2,1)·(1,-1,-2)=0
∴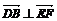 ,
,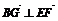 ,又∵BG∩BD=B,∵EF⊥平面GBD.
,又∵BG∩BD=B,∵EF⊥平面GBD.
(2)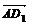 =(-2,0,2),
=(-2,0,2),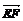 =(1,-1,-2) .
=(1,-1,-2) . 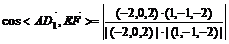 =
=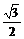 ,
,
即异面直线AD1与EF所成的角为30º.
21.解:(I)
|
正面向上次数m |
3 |
2 |
1 |
0 |
|
概率P(m) |
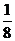 |
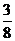 |
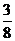 |
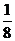 |
|
正面向上次数n |
2 |
1 |
0 |
|
概率P(n) |
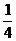 |
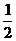 |
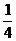 |
(II)甲获胜,则m>n,当m=3时,n=2,1,0,其概率为
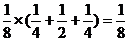
当m=2时,n=1,0. 其概率为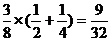
当m=1时,n=0 其概率为
所以,甲获胜的概率为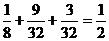
20.解:(I)∵ △ 为以点M为直角顶点的
为以点M为直角顶点的
等腰直角三角形,
 ∴
∴ 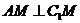 且
且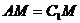 .
.
∵ 正三棱柱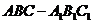 ,
,
∴ 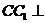 底面ABC.
底面ABC.
∴ 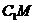 在底面内的射影为CM,AM⊥CM.
在底面内的射影为CM,AM⊥CM.
∵ 底面ABC为边长为a的正三角形,
∴ 点M为BC边的中点.
(II)由(1)知AM⊥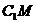 且AM⊥CM,
且AM⊥CM,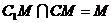 ∴ AM⊥平面
∴ AM⊥平面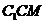 ,
,
过点C作CH⊥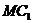 于H, ∵ CH在平面
于H, ∵ CH在平面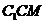 内, ∴ CH⊥AM,
内, ∴ CH⊥AM,
又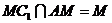 ,有CH⊥平面
,有CH⊥平面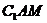 ,
,
即CH为点C到平面AMC1的距离
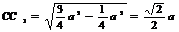 由(1)知,
由(1)知,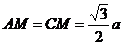 ,
,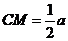 且
且 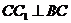 .
.
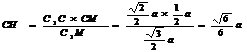
∴ ∴
∴ 点C到平面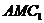 的距离为底面边长为
的距离为底面边长为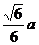 .
.
(III)过点C作CI⊥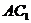 于I,连HI, ∵ CH⊥平面
于I,连HI, ∵ CH⊥平面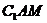 ,
,
∴ HI为CI在平面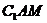 内的射影,
内的射影,
∴ HI⊥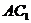 ,故∠CIH是二面角
,故∠CIH是二面角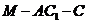 的平面角.
的平面角.
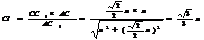
在直角三角形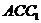 中,
中,
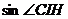

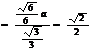 ,
,
∴ ∠CIH=45°, ∴ 二面角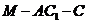 的大小为45°
的大小为45°
19.解:(1)令红色球为x个,则依题意得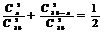 , 所以
, 所以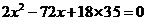 得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
(2)设从袋中任取3个小球,至少有一个红色球的事件为A,均为白色球的事件为B,
则P(B)=1-P(A)=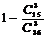 =
=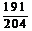
22.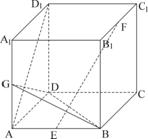 如图正方体在ABCD-A1B1C1D1中,E,F,G分别为AB,B1C1,AA1的中点,
如图正方体在ABCD-A1B1C1D1中,E,F,G分别为AB,B1C1,AA1的中点,
(1) 求证:EF⊥平面GBD;(2) 求异面直线AD1与EF所成的角 .(15分)
21. 甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面(正面)朝上的次数为m,乙用一枚硬币掷2次,记下国徽面(正面)朝上的次数为n.
(I)填写下表
|
正面向上次数m |
3 |
2 |
1 |
0 |
|
概率P(m) |
|
|
|
|
|
正面向上次数n |
2 |
1 |
0 |
|
概率P(n) |
|
|
|
(II)规定m>n时甲胜,求甲获胜的概率。(15分)
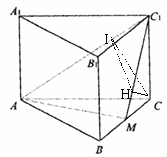
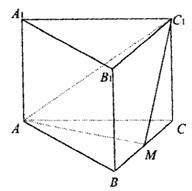
20.如图,正三棱柱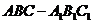 的底面边长为a,点M在边BC上,△
的底面边长为a,点M在边BC上,△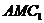
是以点M为直角顶点的等腰直角三角形.(Ⅰ)求证点M为边BC的中点;
(Ⅱ)求点C到平面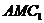 的距离;(Ⅲ)求二面角
的距离;(Ⅲ)求二面角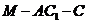 的大小。(15分)
的大小。(15分)
19、口袋里装有红色和白色共36个不同的球,且红色球多于白色球.从袋子中取出2个球,若是同色的概率为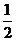 ,求:(1) 袋中红色、白色球各是多少?(2) 从袋中任取3个小球,至少有一个红色球的概率为多少?(15分)
,求:(1) 袋中红色、白色球各是多少?(2) 从袋中任取3个小球,至少有一个红色球的概率为多少?(15分)
18. 给四棱锥V-ABCD的五个面涂颜色,要求相邻的两个面不得使用同一种颜色,现有4种颜色供选择,则不同的涂色方法共有
种(以数字作答). 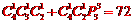 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com