
9.条件甲:平面α内任一直线平行于平面β,条件乙:平面α//平面β,则条件甲是条件乙的A.充分不必要条件 B.必要不充分条件( C )C.充要条件D.既不充分又不必要条件
7.某化工厂实验生产中需依次投入2种化工原料,现已知有5种原料可用,但甲、乙两种原料不能同时使用,且依次投料时,若使用甲原料,则甲必须先投放,因此不同的实验方案共有( C )A.10种 B.12种 C.15种 D.16种
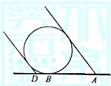 8.当垂直于地面的3m长的木杆影长4m时,水平面上有一圆球,其影子的最远点A距离与地面接触
8.当垂直于地面的3m长的木杆影长4m时,水平面上有一圆球,其影子的最远点A距离与地面接触
点B的长为15m(如右图),则球的体积为( A )
A.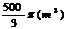 B.
B.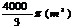
C.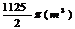 D.
D.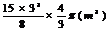
6.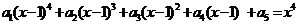 ,则
,则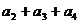 等于AA.
等于AA.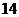 B.
B.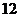 C.
C.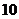 D.
D.
5.正方体与外接球的体积之比为(
C )A.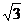 ∶
∶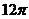 B.
B.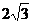 ∶
∶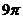 C.
C.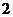 ∶
∶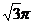 D.
D.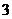 ∶
∶
4.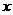 、
、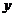 、
、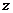 是空间不同的直线或平面,对下列四种情形:①
是空间不同的直线或平面,对下列四种情形:① 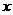 、
、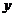 、
、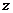 均为直线;②
均为直线;②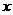 、
、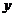 是直线,
是直线,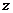 是平面;③
是平面;③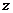 是直线,
是直线,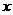 、
、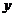 是平面;④
是平面;④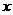 、
、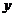 、
、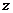 均为平面.其中使“
均为平面.其中使“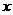 ⊥
⊥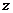 且
且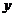 ⊥
⊥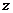
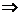
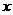 ∥
∥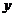 ”为真命题的是A.①② B.① ③ C.③④ D.②③( D
)
”为真命题的是A.①② B.① ③ C.③④ D.②③( D
)
3.运输队有7个车队,每车队的车多于4辆且车型相同,现从这7个车队中抽出10辆,每个车队至少抽1辆,则不同的抽法有A. 种 B.
种 B.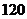 种 C.
种 C. 种 D.
种 D.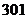 种(
A )
种(
A )
2.对总数为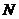 的一批零件抽取一个容量为
的一批零件抽取一个容量为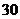 的样本,若每个零件被抽取的概率为
的样本,若每个零件被抽取的概率为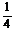 ,则
,则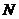 的值为A A.
的值为A A.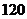 B.
B.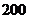 C.
C.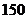 D.
D.
1.已知平面,α,β,γ及直线l,m满足:l⊥m,α⊥γ,γ∩α=m,γ∩β=l,则由此可推出:①β⊥γ,②l⊥α,③m⊥β B A.①和② B.② C.①和③ D.②和③
21. (I)证: 三棱柱中,
又平面,且平面, 平面
(II)证: 三棱柱中, 中
是等腰三角形 ,E是等腰底边的中点,
又依条件知 且
由①,②,③得平面EDB
(III)解: 平面, 且不平行,故延长,ED后必相交, 设交点为E,连接EF,如下图是所求的二面角
依条件易证明 为中点, A为中点
即 又平面EFB, 是所求的二面角的平面角 , E为等腰直角三角形底边中点,
故所求的二面角的大小为 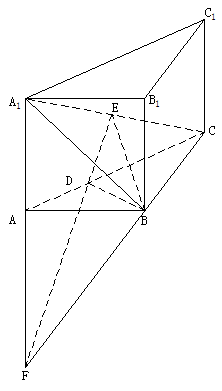
22 证明
证明 (1)当n=1时,42×1+1+31+2=91能被13整除
(1)当n=1时,42×1+1+31+2=91能被13整除
(2)假设当n=k时,42k+1+3k+2能被13整除,则当n=k+1时,
42(k+1)+1+3k+3=42k+1·42+3k+2·3-42k+1·3+42k+1·3
=42k+1·13+3·(42k+1+3k+2?)
∵42k+1·13能被13整除,42k+1+3k+2能被13整除
∴当n=k+1时也成立
由①②知,当n∈N*时,42n+1+3n+2能被13整除
20. 解:(I)设“甲队以3:0获胜”为事件A,则
(II)设“甲队获得总冠军”为事件B,
则事件B包括以下结果:3:0;3:1;3:2三种情况
若以3:0胜,则;
若以3:1胜,则
若以3:2胜,则
所以,甲队获得总冠军的概率为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com