
4.“毒奶粉”事件再次提醒我们要注意食品安全,下列有关食品加工方法安全的是
A.用工业盐(含NaNO2)来做食品添加剂
B.用塑料颗粒来制作珍珠奶茶中的“珍珠”
C.用工业酒精勾兑水来生产低成本白酒
D.用小苏打来作焙制糕点的发酵粉成分
3.“神七”太空舱利用NiFe2O4做催化剂将宇航员呼出的CO2转化为O2,已知Fe 的化合价为+3,则Ni 的化合价为
A.+1 B.+2 C.+3 D.+4
2.下列物质与水混合充分搅拌后能导电的是
A.氢氧化铜 B.酒精 C.食盐 D.氯化银
1.下列在厨房中发生的变化是物理变化的是
A.榨取果汁 B.冬瓜腐烂 C.铁锅生锈 D.煤气燃烧
29.问题解决
解:方法一:如图(1-1),连接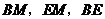 .
.
由题设,得四边形 和四边形
和四边形 关于直线
关于直线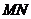 对称.
对称.
∴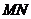 垂直平分
垂直平分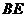 .∴
.∴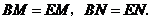 ··········································· 1分
··········································· 1分
∵四边形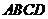 是正方形,∴
是正方形,∴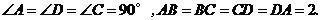
∵ 设
设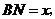 则
则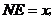
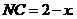
在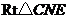 中,
中,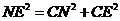 .
.
∴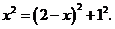 解得
解得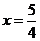 ,即
,即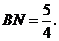 ················································ 3分
················································ 3分
在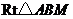 和在
和在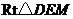 中,
中,
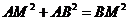 ,
,
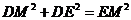 ,
,
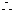
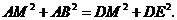 ······································································· 5分
······································································· 5分
设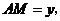 则
则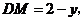 ∴
∴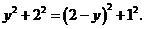
解得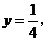 即
即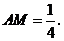 ················································································· 6分
················································································· 6分
∴ ··································································································· 7分
··································································································· 7分
方法二:同方法一,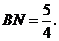 ········································································· 3分
········································································· 3分
如图(1-2),过点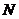 做
做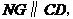 交
交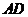 于点
于点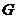 ,连接
,连接
∵ ∴四边形
∴四边形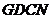 是平行四边形.
是平行四边形.
∴
同理,四边形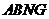 也是平行四边形.∴
也是平行四边形.∴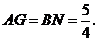
∵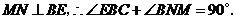
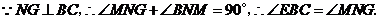
在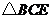 与
与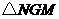 中
中
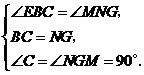 ∴
∴ ····························· 5分
····························· 5分
∵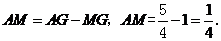 ······························································ 6分
······························································ 6分
∴ ································································································· 7分
································································································· 7分
类比归纳
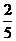 (或
(或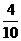 );
);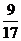 ;
; 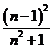 ·········································································· 10分
·········································································· 10分
联系拓广
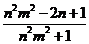 ···································································································· 12分
···································································································· 12分
26.(1)解:由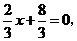 得
得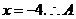 点坐标为
点坐标为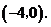
由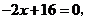 得
得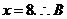 点坐标为
点坐标为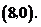
∴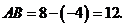 ··················································································· (2分)
··················································································· (2分)
由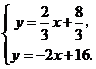 解得
解得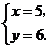 ∴
∴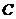 点的坐标为
点的坐标为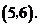 ···································· (3分)
···································· (3分)
∴ ··························································· (4分)
··························································· (4分)
(2)解:∵点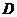 在
在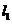 上且
上且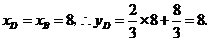
∴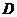 点坐标为
点坐标为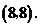 ······················································································ (5分)
······················································································ (5分)
又∵点 在
在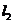 上且
上且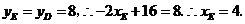
∴ 点坐标为
点坐标为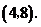 ······················································································ (6分)
······················································································ (6分)
∴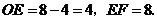 ··········································································· (7分)
··········································································· (7分)
(3)解法一: 当
当 时,如图1,矩形
时,如图1,矩形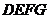 与
与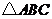 重叠部分为五边形
重叠部分为五边形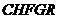 (
(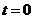 时,为四边形
时,为四边形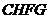 ).过
).过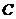 作
作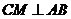 于
于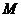 ,则
,则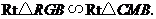

∴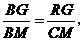 即
即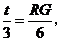 ∴
∴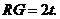
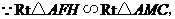
∴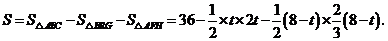
即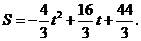 ··································································· (10分)
··································································· (10分)
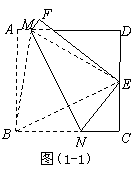
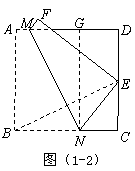
(2009年山西省太原市)29.(本小题满分12分)
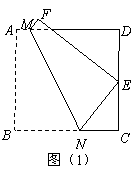 问题解决
问题解决
如图(1),将正方形纸片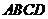 折叠,使点
折叠,使点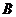 落在
落在 边上一点
边上一点 (不与点
(不与点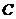 ,
,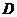 重合),压平后得到折痕
重合),压平后得到折痕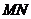 .当
.当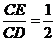 时,求
时,求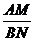 的值.
的值.

类比归纳
在图(1)中,若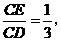 则
则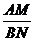 的值等于 ;若
的值等于 ;若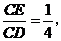 则
则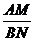 的值等于 ;若
的值等于 ;若 (
(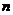 为整数),则
为整数),则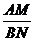 的值等于 .(用含
的值等于 .(用含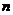 的式子表示)
的式子表示)
联系拓广
如图(2),将矩形纸片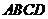 折叠,使点
折叠,使点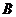 落在
落在 边上一点
边上一点 (不与点
(不与点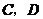 重合),压平后得到折痕
重合),压平后得到折痕 设
设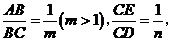 则
则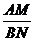 的值等于 .(用含
的值等于 .(用含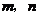 的式子表示)
的式子表示)

26.(2009年山西省)(本题14分)如图,已知直线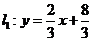 与直线
与直线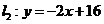 相交于点
相交于点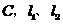 分别交
分别交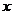 轴于
轴于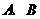 两点.矩形
两点.矩形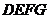 的顶点
的顶点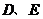 分别在直线
分别在直线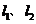 上,顶点
上,顶点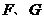 都在
都在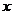 轴上,且点
轴上,且点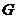 与点
与点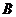 重合.
重合.
(1)求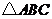 的面积;
的面积;
(2)求矩形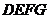 的边
的边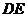 与
与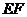 的长;
的长;
(3)若矩形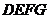 从原点出发,沿
从原点出发,沿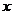 轴的反方向以每秒1个单位长度的速度平移,设
轴的反方向以每秒1个单位长度的速度平移,设
移动时间为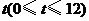 秒,矩形
秒,矩形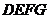 与
与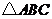 重叠部分的面积为
重叠部分的面积为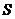 ,求
,求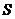 关
关

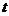 的函数关系式,并写出相应的
的函数关系式,并写出相应的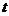 的取值范围.
的取值范围.
23.(2009年河南省)(11分)如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标,并求出抛物线的解析式;
(2)动点P从点A出发.沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD
向终点D运动.速度均为每秒1个单位长度,运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F,交抛物线于点G.当t为何值时,线段EG最长?
②连接EQ.在点P、Q运动的过程中,判断有几个时刻使得△CEQ是等腰三角形?
请直接写出相应的t值.

解.(1)点A的坐标为(4,8) …………………1分
将A (4,8)、C(8,0)两点坐标分别代入y=ax2+bx
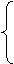 8=16a+4b
8=16a+4b
得
0=64a+8b
解 得a=-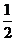 ,b=4
,b=4
∴抛物线的解析式为:y=-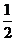 x2+4x
…………………3分
x2+4x
…………………3分
(2)①在Rt△APE和Rt△ABC中,tan∠PAE=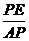 =
=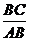 ,即
,即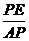 =
=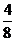
∴PE=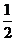 AP=
AP=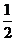 t.PB=8-t.
t.PB=8-t.
∴点E的坐标为(4+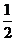 t,8-t).
t,8-t).
∴点G的纵坐标为:-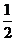 (4+
(4+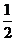 t)2+4(4+
t)2+4(4+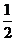 t)=-
t)=-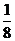 t2+8. …………………5分
t2+8. …………………5分
∴EG=-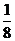 t2+8-(8-t)
t2+8-(8-t)
=-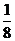 t2+t.
t2+t.
∵-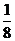 <0,∴当t=4时,线段EG最长为2.
…………………7分
<0,∴当t=4时,线段EG最长为2.
…………………7分
②共有三个时刻. …………………8分
t1=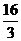 , t2=
, t2=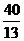 ,t3=
,t3= 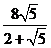 .
…………………11分
.
…………………11分
26. 解:(1)1,
解:(1)1,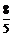 ;
;
(2)作QF⊥AC于点F,如图3, AQ = CP= t,∴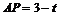 .
.
由△AQF∽△ABC, ,
,
得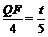 .∴
.∴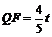 .
.
 ∴
∴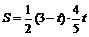 ,
,
即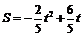 .
.
(3)能.
①当DE∥QB时,如图4.
∵DE⊥PQ,∴PQ⊥QB,四边形QBED是直角梯形.
此时∠AQP=90°.
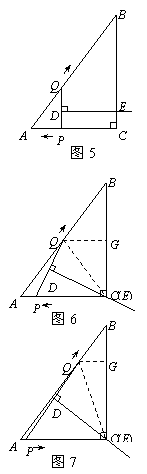 由△APQ ∽△ABC,得
由△APQ ∽△ABC,得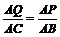 ,
,
即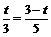 . 解得
. 解得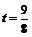 .
.
②如图5,当PQ∥BC时,DE⊥BC,四边形QBED是直角梯形.
此时∠APQ =90°.
由△AQP ∽△ABC,得 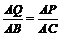 ,
,
即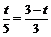 . 解得
. 解得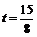 .
.
(4)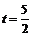 或
或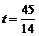 .
.
[注:①点P由C向A运动,DE经过点C.
方法一、连接QC,作QG⊥BC于点G,如图6.
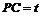 ,
,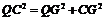
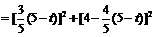 .
.
由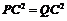 ,得
,得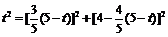 ,解得
,解得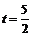 .
.
方法二、由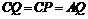 ,得
,得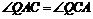 ,进而可得
,进而可得
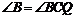 ,得
,得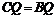 ,∴
,∴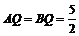 .∴
.∴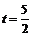 .
.
②点P由A向C运动,DE经过点C,如图7.
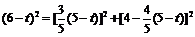 ,
,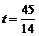 ]
]
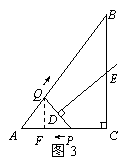
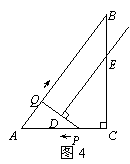
26.(2009年河北省)(本小题满分12分)
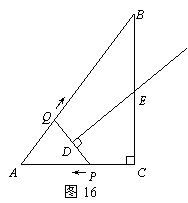 如图16,在Rt△ABC中,∠C=90°,AC = 3,AB
= 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
如图16,在Rt△ABC中,∠C=90°,AC = 3,AB
= 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)当t = 2时,AP = ,点Q到AC的距离是 ;
(2)在点P从C向A运动的过程中,求△APQ的面积S与
t的函数关系式;(不必写出t的取值范围)
(3)在点E从B向C运动的过程中,四边形QBED能否成
为直角梯形?若能,求t的值.若不能,请说明理由;
(4)当DE经过点C 时,请直接写出t的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com