
4.右图是一种升降电梯的示意图,A为载人箱,B为平衡重物,它们的质量均为M,上下均有跨过滑轮的钢索系住,在电动机的牵引下使电梯上下运动.如果电梯中载人的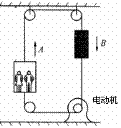 质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止,在不计空气和摩擦阻力的情况下,h为
质量为m,匀速上升的速度为v,电梯即将到顶层前关闭电动机,依靠惯性上升h高度后停止,在不计空气和摩擦阻力的情况下,h为
A.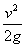 B.
B.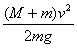 C.
C.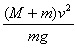 D.
D.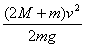
3. 如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,∠ABC=β.AB边及AC两边上分别套有用细线相连的铜环(其总长度小于BC边长),当它们静止时,细线跟AB所成的角θ的大小为( )
如图所示,用光滑的粗铁丝做成一直角三角形,BC边水平,AC边竖直,∠ABC=β.AB边及AC两边上分别套有用细线相连的铜环(其总长度小于BC边长),当它们静止时,细线跟AB所成的角θ的大小为( )
A.θ=β B.θ=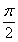 C.θ<β D.β<θ<
C.θ<β D.β<θ<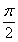
2.如图所示,一个小球(视为质点)从H=12m高处,由静止开始通过光滑弧形轨道AB,进入半径R=4m的竖直圆环,圆环轨道部分的动摩擦因数处处相等,当到达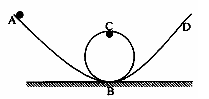 环顶C时,刚好对轨道压力为零;沿CB滑下后,进入光滑弧形轨道BD,且到达高度为h的D点时速度为零,则h之值可能为(g=10m/s2)
环顶C时,刚好对轨道压力为零;沿CB滑下后,进入光滑弧形轨道BD,且到达高度为h的D点时速度为零,则h之值可能为(g=10m/s2)
A.10m B.11m C.8m D.9m
1、如图所示,质量相同的两个带电粒子P、Q以相同的初速度沿垂直于电场方向射入两平行板间的匀强电场中,P从两极板正中央射入,Q从下极板边缘处射入,它们最后打在同一 点(重力不计),则从开始射入到打到上极板的过程中
点(重力不计),则从开始射入到打到上极板的过程中
A、 它们运动的时间tQ = tP
B、 它们所带电荷量之比qp : qQ = 1 : 2
C、它们的电势能减少量之比△EP : △EQ = 1: 2
D、它们的动量增量之比△Pp : △PQ = 2 : 1
22.(本小题满分12分)设函数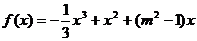 ,其中,
,其中,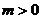
(1) 求函数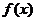 的单调区间与极值;
的单调区间与极值;
(2) 已知函数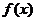 有3个不同的零点0,x1,x2,且x1<x2,若对任意的x∈[x1,x2],
有3个不同的零点0,x1,x2,且x1<x2,若对任意的x∈[x1,x2], 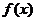 >
>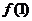 恒成立,求
恒成立,求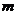 的取值范围
的取值范围
21.(本小已知函数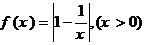
(1)当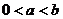 ,且
,且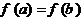 时,求证:
时,求证: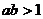
(2)是否存在实数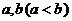 ,使得函数
,使得函数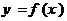 的定义域、值域都是
的定义域、值域都是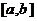 ?若存在,则求出
?若存在,则求出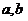 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
20. (本小题满分12分)设函数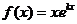 (
(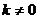 )
)
(1)求曲线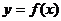 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(3) 求函数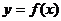 的单调区间;
的单调区间;
(3)若函数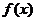 在区间(-1,1)内单调递增,求
在区间(-1,1)内单调递增,求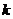 的取值范围
的取值范围
19.
(本小题满分12分).若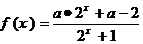 为奇函数。
为奇函数。
(1)判断它的单调性;
(2)求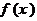 的值域.
的值域.
18. (本小题满分12分) 甲、乙二人进行一次围棋比赛,约定先胜三局者获得这次比赛胜利,比赛结束.假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4.各局比赛相互独立.已知前2局中甲乙各胜一局.
(1)甲获得这次比赛胜利的概率;
(2)设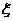 表示从第3局开始到比赛结束所进行的局数,求
表示从第3局开始到比赛结束所进行的局数,求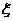 的分布列及数学期望
的分布列及数学期望
17.(本小题满分10分)已知关于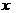 的不等式
的不等式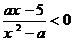 的解集为
的解集为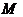 。
。
(1)当 时,求集合
时,求集合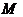 ;
;
(2)若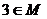 且
且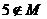 ,求实数
,求实数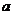 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com