
(三).信息交流 揭示规律
问题2的解决:(学生拿自己的草稿在投影下讲)
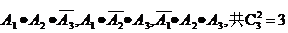 分别记在第1,2,3次射击中,该同学击破气球为事件A1,A2,A3,那么射击3次,击破2个共有下面三种情况:,
种,每一种情况的概率为
分别记在第1,2,3次射击中,该同学击破气球为事件A1,A2,A3,那么射击3次,击破2个共有下面三种情况:,
种,每一种情况的概率为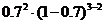 ,因为三种情况彼此互斥,故3次射击击破2个的概率
,因为三种情况彼此互斥,故3次射击击破2个的概率
|
x |
0 |
1 |
2 |
3 |
|
p |
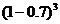 |
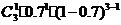 |
 |
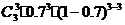 |
X的分布列:
而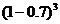 +
+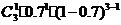 +
+ +
+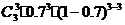
=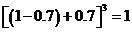
设计意图: 上述解答是一个前面所学知识的应用过程 . 学生看到最后的结果,有一种``拨开云雾看清天”的感觉,这不就是二项式定理吗?学生热情高涨,课堂达到高潮,把对知识的学习掌握变成了对知识的探索 、发现、总结、创新的过程.
通过解决问题2,学生在老师引导下,由特殊到一般,由具体到抽象,由n次独立重复试验发生k次的概率,主动建构二项分布这一重要的离散型随机变量的分布列.攻破本节课的难点。
2.二项分布模型的构建(这一过程师生共同完成):
若一次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生K次的概率为. 

以事件A发生的次数X为随机变量,则X的分布列为:



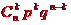
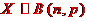 其中的
是二项式
展开式中的通项,故称X服从二项分布。记为
,其中 n,p 为参数, n表示重复的次数,p指一次试验中事件A发生的概率。
其中的
是二项式
展开式中的通项,故称X服从二项分布。记为
,其中 n,p 为参数, n表示重复的次数,p指一次试验中事件A发生的概率。
深化认识:
二项分布是一种概率模型,有着十分广泛的应用。用以解决独立重复试验中的概率问题.比如下列问题中的随机变量ξ都可以看作是服从二项分布的:
n n次独立射击,每次命中率相同,ξ为命中次数。
n 一枚硬币掷n次,ξ为正面出现的次数。
n 掷n个相同的骰子,ξ为一点出现的次数。
n n个新生婴儿,ξ为男婴的个数。
n 女性患色盲的概率为0.25%,ξ为任取n个女人中患色盲的人数。(这一过程约8分钟)
设计意图:从实际中来,到实际中去,抽象出的二项分布有何用途?什么时候用?这是学生想知道的。也是我们学习数学的目的所在。
怎么用呢?导入下一个环节。
(一).创设情景 激发求知
1、投掷一枚相同的硬币5次,每次正面向上的概率为0.5。
2、某同学玩射击气球游戏,每次射击击破气球的概率为0.7,现有气球10个。
3、某篮球队员罚球命中率为0.8,罚球6次。
4、口袋内装有5个白球、3个黑球,不放回地抽取5个球。
问题1、上面这些试验有什么共同的特点?
设计意图:
利用学生求知好奇心理,以一个个人人皆知的试验为切入点,便于激发学生学习本节课的兴趣,调动学生思维的积极性。紧扣本节课教学内容的主题与重点, 有利于知识的迁移,使学生明确知识的实际应用性。了解数学来源于实际。
①包含了n个相同的试验。②每次试验相互独立。③每次试验只有两种可能的结果:“成功”或“失败”。④每次出现“成功”的概率p相同,“失败“的概率也相同,为1-p。⑤试验”成功”或“失败”可以计数,即试验结果对应于一个离散型随机变量。
我们把这样的试验叫做独立重复试验。
1、独立重复试验:
一般的,在相同条件下重复做的n次试验称为n次独立重复试验.
强调:
⑴独立重复试验,是在相同条件下各次之间相互独立地进行的一种试验;
⑵每次试验只有“成功”或“失败”两种可能结果。每次试验“成功”的概率都p ,“失败”的概率为1-p.
设计意图:水到渠成!学生由实例抽象出独立重复试验的概念.尝试到成功的喜悦。达到第一个目标;学生理解了独立重复试验,又培养了学生观察、分析、总结、归纳的能力。(到此约用6-7分钟)
此时学生具有强烈的求知欲,注意力高度集中,等着解决下一个问题。
我顺势提出第二个问题:
问题2. 某同学玩射击气球游戏,若每次射击击破气球的概率为0.7,每次射击结果互不影响,现有气球3个, 恰好击破2个的概率是多少?设击破气球的个数为X,X的分布列怎样?
进入第二个环节. (二).自主探究 合作学习
设计意图: 前节课已经解决了相互独立事件概率的求法,这个问题大部分学生能够独立解决。解决问题过程中,允许讨论。老师巡视,参与其中,适当指导,解答学生提问.5-6分钟学生跃跃欲试,纷纷举手示意.选一过程写得较详细清楚的同学代表展示自己的解答过程.
本节课我设计为五个环节:
1.创设情景 激发求知
2.自主探究 合作学习
3.信息交流 揭示规律
4.运用规律 解决问题
5.提炼方法 反思小结
可以循环使用.多媒体辅助贯穿整个教学过程.
学是中心,学会是目的.本节课主要让学生体会观察、分析、归纳、抽象、应用的自主探究式学习方法.交给学生思考问题的方法,使学生真正成为教学的主体.
自主性、能动性是人的各种潜能中最主要也是最高层次的潜能,教育只有在尊重学生主体的基础上,才能激发学生的主体意识,培养学生的主体精神和主体人格,“主体”参与是现代教学论关注的要素 。我在课堂教学中做到以学生的自主学习为中心,给学生提供尽可能多的思考、探索、发现、想象、创新的时间和空间。另一方面,从学生的认知结构,预备知识的掌握情况,我班学生有自主学习、主动构建新知识的能力。
由此,本节课主要采取“自主探究式”的教学方法:即学生在老师引导下,观察发现、自主探究、合作交流、由特殊到一般、由感性到理性主动建构新知识。启发引导学生积极的思维,对学生的思维进行调控,帮助学生优化思维过程。
教学手段:多媒体辅助教学,激发学生的学习兴趣,增大课堂容量,提高课堂教学效果。
3.教学重点、难点:
数学建模是运用数学思想、方法和知识解决实际问题的过程,是数学学习的一种新的方式,它为学生提供自主学习的空间,有助于学生体验数学在解决实际问题中的价值和作用。高二学生虽然具有一定的抽象思维能力,但是从实际中抽象出数学模型对于学生来说还是比较困难的,需要老师的正确引导。由此制定出本节课的重难点如下:
教学重点:独立重复试验、二项分布的理解及应用二项分布模型解决一些简单的实际问题。
教学难点:二项分布模型的构建。
重难点的突破将在教学程序分析中详述。
2.教学目标:
知识目标:
高中数学新教学大纲明确指出本节课需达到的知识目标:在了解条件概率和相互独立事件概念的前提下,理解n次独立重复试验的模型及二项分布,并能解决一些简单的实际问题。
同时,渗透由特殊到一般,由具体到抽象,观察、分析、类比、归纳的数学思想方法。
能力目标:
培养学生的自主学习能力、数学建模能力和应用数学知识解决实际问题的能力。
德育目标:
培养学生对新知识的科学态度,勇于探索和敢于创新的精神。让学生了解数学来源于实际,应用于实际的唯物主义思想。
情感目标:
通过主动探究、合作学习、相互交流,感受探索的乐趣与成功的喜悦,体会数学的理性与严谨,养成实事求是的科学态度和契而不舍的钻研精神。
1.教材的地位和作用
本节内容是新教材选修2-3第二章《随机变量及其分布》的第二节《二项分布及其应用》的第三小节。通过前面的学习,学生已经学习掌握了有关概率和统计的基础知识:等可能事件概率、互斥事件概率、条件概率、相互独立事件概率的求法以及分布列有关内容。二项分布是继超几何分布后的又一应用广泛的概率模型,而超几何分布在产品数量n相当大时可以近似的看成二项分布。在自然现象和社会现象中,大量的随机变量都服从或近似的的服从二项分布,实际应用广泛,理论上也非常重要。可以说本节内容是对前面所学知识的综合应用,是一种模型的构建。是从实际入手,通过抽象思维,建立数学模型,进而认知数学理论,应用于实际的过程。会对今后数学及相关学科的学习产生深远的影响。
25.东莞一研究性学习小组,对地球运动及其产生的地理现象进行探究时遇到了一些问题,请结合所学地理知识予以解答。(9分)
|
遇到问题 |
解答问题 |
|
(1)他们认为:在一个窗户朝正南的房间里,全年正午阳光都能照射到房内。你认为是否正确?为什么? |
|
(2)他们在进行图像转换时遇到了困难,请将下图所示内容按要求转绘在右图中。 |
(要求:在下图中绘出晨昏线、用阴影表示夜半球部分、标出直射点所在经线的经度。)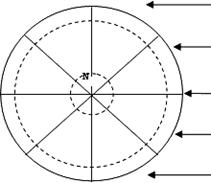 |
24.读图回答下列问题。(13分)

(1)甲区域所在国常发生洪涝灾害,分析其形成的主要原因。(4分)
(2)乙区域气候类型为 ,气候特征是 。(4分)
(3)丙区域的气候特征与同纬度同类气候相比主要有哪些不同点? (2分)
(4)丁区域所在国的地形特征是 。(3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com