热学是物理学的一个组成部分，它研究的是热现象的规律。描述热现象的一个基本概念是温度。凡是跟温度有关的现象都叫做热现象。分子动理论是从物质微观结构的观点来研究热现象的理论。它的基本内容是：物体是由大量分子组成的；分子永不停息地做无规则运动；分子间存在着相互作用力。

1.物体是由大量分子组成的

这里的分子是指构成物质的单元，可以是原子、离子，也可以是分子。在热运动中它们遵从相同的规律，所以统称为分子。

⑴这里建立了一个理想化模型：把分子看作是小球，所以求出的数据只在数量级上是有意义的。一般认为分子直径大小的数量级为10^-10m。

⑵固体、液体被理想化地认为各分子是一个挨一个紧密排列的，每个分子的体积就是每个分子平均占有的空间。分子体积=物体体积÷分子个数。

⑶气体分子仍视为小球，但分子间距离较大，不能看作一个挨一个紧密排列，所以气体分子的体积远小于每个分子平均占有的空间。每个气体分子平均占有的空间看作以相邻分子间距离为边长的正立方体。

⑷阿伏加德罗常数NA=6.02×10²³mol^-1，是联系微观世界和宏观世界的桥梁。它把物质的摩尔质量、摩尔体积这些宏观物理量和分子质量、分子体积这些微观物理量联系起来了。

例1. 根据水的密度为ρ=1.0×10³kg/m³和水的摩尔质量M=1.8×10^-2kg,，利用阿伏加德罗常数，估算水分子的质量和水分子的直径。

解：每个水分子的质量m=M/N_A=1.8×10^-2÷6.02×10²³=3.0×10^-26kg；水的摩尔体积V=M/ρ，把水分子看作一个挨一个紧密排列的小球，则每个分子的体积为v=V/N_A,而根据球体积的计算公式，用d表示水分子直径，v=4πr³/3=πd³/6，得d=4×10^-10 m

例2. 利用阿伏加德罗常数，估算在标准状态下相邻气体分子间的平均距离D。

解：在标准状态下， 1mol任何气体的体积都是V=22.4L，除以阿伏加德罗常数就得每个气体分子平均占有的空间，该空间的大小是相邻气体分子间平均距离D的立方。

，这个数值大约是分子直径的10倍。因此水气化后的体积大约是液体体积的1000倍。

6. 若ΔABC的三边长分别为m²-n²，m²⁺n²，2mn。(m>n>0)求证：ΔABC是直角三角形

5. 如图已知： △ABC中，∠ABC的平分线与∠ACB的外角平分线交于D，DE∥BC交AB于E，交AC于F。求证：BE=EF+CF

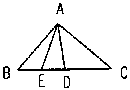
4. 如图已知： △ABC中，BC=2AB，D、E分别是BC、BD的中点。求证：AC=2AE

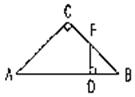
3. 如图已知：RtΔABC中，C=90°，DE⊥AB于D，BC=1，AC=AD=1。求：DE、BE的长。

2、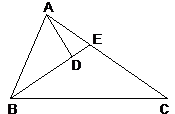如图，在锐角△ABC中，∠ABC＝2∠C，∠ABC的平分线与AD垂直，垂足为D，求证：AC＝2BD。

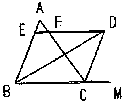
1.如图，已知∠MON的边OM上有两点A、B，边ON上有两点C、D，且AB＝CD，P为∠MON的平分线上一点。问：

(1)△ABP与△PCD是否全等？请说明理由。

(2)△ABP与△PCD的面积是否相等？请说明理由。

6. 如图已知：△ABC中，AB=AC，AB的垂直平分线DE交AC于E，垂足为D，如果∠A=40˚，那么∠BEC=　　 ；如果△BEC的周长为20cm，那么底边BC=　　　 。

5. 如图已知：AD是△ABC的对称轴，如果∠DAC=30˚，DC=4cm，

那么△ABC的周长为　　　 cm。

4. 如图已知：△ABC≌△DBE，∠A=50°，∠E=30°

则∠ADB=　　 度，∠DBC=　　 度