6、构造法：在解题时，我们常常会采用这样的方法，通过对条件和结论的分析，构造辅助元素，它可以是一个图形、一个方程(组)、一个等式、一个函数、一个等价命题等，架起一座连接条件和结论的桥梁，从而使问题得以解决，这种解题的数学方法，我们称为构造法。运用构造法解题，可以使代数、三角、几何等各种数学知识互相渗透，有利于问题的解决。

5、待定系数法：在解数学问题时，若先判断所求的结果具有某种确定的形式，其中含有某些待定的系数，而后根据题设条件列出关于待定系数的等式，最后解出这些待定系数的值或找到这些待定系数间的某种关系，从而解答数学问题，这种解题方法称为待定系数法。它是中学数学中常用的重要方法之一。

4、判别式法与韦达定理：一元二次方程ax2+bx+c=0(a、b、c∈R，a≠0)根的判别式△=b2-4ac，不仅用来判定根的性质，而且作为一种解题方法，在代数式变形，解方程(组)，解不等式，研究函数乃至解析几何、三角函数运算中都有非常广泛的应用。

　韦达定理除了已知一元二次方程的一个根，求另一根；已知两个数的和与积，求这两个数等简单应用外，还可以求根的对称函数，计论二次方程根的符号，解对称方程组，以及解一些有关二次曲线的问题等，都有非常广泛的应用。

3、换元法：换元法是数学中一个非常重要而且应用十分广泛的解题方法。我们通常把未知数或变数称为元，所谓换元法，就是在一个比较复杂的数学式子中，用新的变元去代替原式的一个部分或改造原来的式子，使它简化，使问题易于解决。

2、因式分解法：因式分解，就是把一个多项式化成几个整式乘积的形式。因式分解是恒等变形的基础，它作为数学的一个有力工具、一种数学方法在代数、几何、三角函数等的解题中起着重要的作用。因式分解的方法有许多，除中学课本上介绍的提取公因式法、公式法、分组分解法、十字相乘法等外，还有如利用拆项添项、求根分解、换元、待定系数等等。

1、配方法：所谓配方，就是把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和形式。通过配方解决数学问题的方法叫配方法。其中，用的最多的是配成完全平方式。配方法是数学中一种重要的恒等变形的方法，它的应用非常广泛，在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它。

21、(本题满分14分)如图①，正方形ABCD的顶点A,B的坐标分别为(0，10)，(8，4)，，顶点C，D在第一象限，点P从点A出发，沿正方形按逆时针方向匀速运动，同时，点Q从点E(4，0)出发，沿x轴正方向以相同速度运动，当点P到达点C时，P,Q两点同时停止运动，设运动时间为t秒。

⑴、求正方形ABCD的边长？

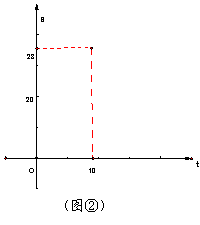
⑵、当点P在AB边上运动时，△OPQ的面积S(平方单位)与时间t(秒)之间的函数图像为抛物线的一部分(如图②所示)，求P,Q两点的运动速度？

⑶、求⑵中面积S与时间t的函数关系式及面积S取最大值时点P的坐标？

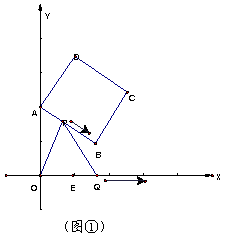
⑷、若点P,Q保持⑵中的速度不变，则点P沿着AB边运动时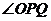，的大小随着时间t的增大而增大，沿着BC边运动时，的大小随着时间t的增大而减小，当点P沿着这两边运动时，使=90°的点P有几个，并说明理由？

	(第19题图)

20、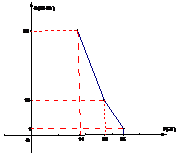(本题满分11分)对口扶贫活动中，为了尽快脱贫(无债务)致富，企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型残疾人企业乙，并约定从该店经营的利润中，首先保证企业乙的全体职工每个月最低的生活费的开支3600元后，逐步偿还转让费(不计息)，在甲提供的材料中有：①这种消费品的进价每件14元；②该店月销量Q(百件)与销售价格P(元)的关系如图；③每月需各种开支2000元。

⑴、为使该店刚好能够维持职工生活，商品的价格应定为多少？

最大？并求出最大值。

⑶、企业乙只依靠该店，最早可望在几年后脱贫？

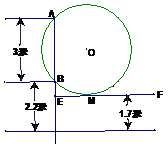
19、(本题满分7分)1471年，德国数学家米勒提出了雕塑问题：假定有一个雕塑高AB=3米，立在一个底座上，底座的高BC=2.2米，一个人注视着这个雕塑并朝它走去，这个人的水平视线离地1.7米，问此人应站在离雕塑底座多远处，才能使看雕塑的效果最好，所谓看雕塑的效果最好是指看雕塑的视角最大，问题转化为在水平视线EF上求使视角最大的点，如图：过A、B两点，作一圆与EF相切于点M，你能说明点M为所求的点吗？并求出此时这

个人离雕塑底座的距离？

18、(本题满分7分) 糖业是我省重要的生物资源产业，我省一糖业集团今年4月收购甘蔗后入榨甘蔗250万吨，榨糖率为12﹪，经市场调查知5月份糖的销售价为2940元/吨，若糖业集团在5月销售4月份生产的糖，产销率为60﹪；又知糖业集团若在6月，7月两个月内销售4月生产的糖，销售价将在5月的基础上每月比上月降低6﹪，糖销量将在5月的基础上每月比上月增加9﹪.

⑴、问2005年4月糖业集团生产了多少吨糖？

⑵、若糖业集团计划只在7月销售4月生产的糖，请求出该糖业集团7月销售4月生产的糖的销售额是多少？(精确到万元)

( 榨糖率＝产糖量÷入榨甘蔗量×100﹪，产销率＝糖销量÷产糖量×100﹪，销售额＝销售单价×销售数量)