
1、一个动点在三棱锥体内等可能出现,则该动点与下底面构成的三棱锥的体积超过原三棱锥体积的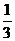 而不足原三棱锥体积的
而不足原三棱锥体积的 的概率为D A、
的概率为D A、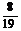 ; B、
; B、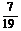 ; C、
; C、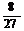 ; D、
; D、 ;
;
22.(1)解:设数列{bn}的公差为d,由题意得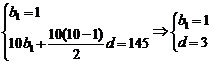 ,∴bn=3n-2
,∴bn=3n-2
(2)证明:由bn=3n-2知
Sn=loga(1+1)+loga(1+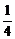 )+…+loga(1+
)+…+loga(1+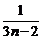 )
)
=loga[(1+1)(1+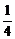 )…(1+
)…(1+ 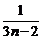 )]
)]
而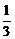 logabn+1=loga
logabn+1=loga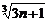 ,于是,比较Sn与
,于是,比较Sn与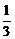 logabn+1?的大小
logabn+1?的大小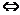 比较(1+1)(1+
比较(1+1)(1+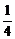 )…(1+
)…(1+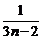 )与
)与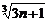 的大小.
的大小.
取n=1,有(1+1)=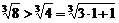
取n=2,有(1+1)(1+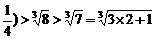
推测:(1+1)(1+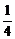 )…(1+
)…(1+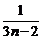 )>
)>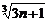 (*)
(*)
①当n=1时,已验证(*)式成立.
②假设n=k(k≥1)时(*)式成立,即(1+1)(1+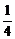 )…(1+
)…(1+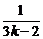 )>
)>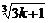
则当n=k+1时,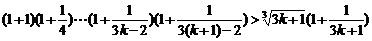
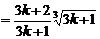
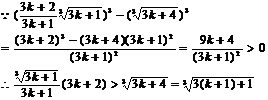
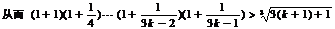 ,即当n=k+1时,(*)式成立,由①②知,(*)式对任意正整数n都成立.于是,当a>1时,Sn>
,即当n=k+1时,(*)式成立,由①②知,(*)式对任意正整数n都成立.于是,当a>1时,Sn>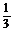 logabn+1?,当 0<a<1时,Sn<
logabn+1?,当 0<a<1时,Sn<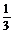 logabn+1?
logabn+1?
21.解:(I)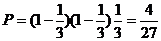
(II)依题意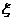 ~
~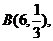
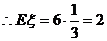 9分
9分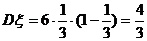 …
…
19.解(Ⅰ)由已知有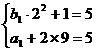 , 解得b1=1, a1=-13.
, 解得b1=1, a1=-13.
从而an =-13+(n-1)·2=2 n-15, bn=1×2 n-1=2 n-1, cn= anbn=(2n-15)2 n-1.
(Ⅱ) ∵Sn= a1b1+ a2b2+…+anbn, ①
qSn= a1b2+ a2b3+…+anbn+1. ②.
①-②得(1-q)Sn= a1b1+d( b2 +b3+…+bn)-
anbn+1= a1b1+ d·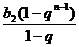 -
anbn+1
-
anbn+1
=-13+2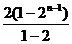 -(2n-15)2
n=-[(2n-17) 2 n+17],
-(2n-15)2
n=-[(2n-17) 2 n+17],
∴Sn=(2n-17) 2 n+17.
∴
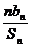 =
=
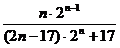 =
= =
=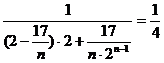
22.已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+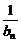 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与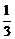 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
21.一名学生骑自行车上学,从他的家到学校的途中有6个交通岗,假设他在各交通岗遇到红灯的事件是独立的,并且概率都是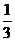 .(I)求这名学生首次遇到红灯前,已经过了两个交通岗的概率;
.(I)求这名学生首次遇到红灯前,已经过了两个交通岗的概率;
(II)求这名学生在途中遇到红灯数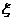 的期望与方差.
的期望与方差.
20.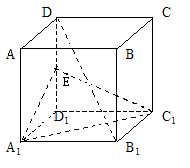 正方体
正方体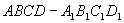 中,点E是
中,点E是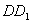 的中点,如图,
(1)求证:
的中点,如图,
(1)求证: ;
(2)求证:
;
(2)求证: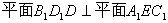 ;
(3)求证:
;
(3)求证: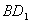 不垂直于平面
不垂直于平面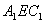 。
。
19.{an}为等差数列, 公差为d, {bn}为等比数列, 公比为q且d= q=2, b3+1= a10=5, 设cn= anbn.(Ⅰ)求数列{cn}的通项公式; (Ⅱ)设数列{cn}的前n项和为Sn,求
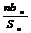 的值.
的值.
18、甲、乙两人各进行1次射击,甲击中目标的概率是0.8,乙击中目标的概率是0.7,则甲乙都击中的概率是 .0.56
17.将棱长为1的正方体木块加工成一个体积最大的球,则这个球的体积为__________,球的表面积为_________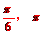
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com