
2.直线方程的五种形式:
(1)点斜式: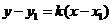 (直线
(直线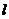 过点
过点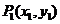 ,且斜率为
,且斜率为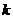 ).
).
(2)斜截式: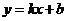 (
(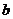 为直线
为直线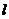 在
在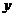 轴上的截距).
轴上的截距).
(3)两点式: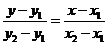 (
(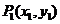 、
、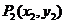
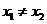 ,
,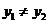 ).
).
(4)截距式: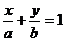 (其中
(其中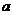 、
、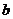 分别为直线在
分别为直线在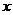 轴、
轴、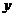 轴上的截距,且
轴上的截距,且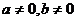 ).
).
(5)一般式: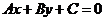 (其中A、B不同时为0).
(其中A、B不同时为0).
1.斜率公式: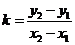 ,其中
,其中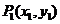 、
、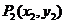 .
.
直线的方向向量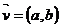 ,则直线的斜率为
,则直线的斜率为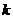 =
=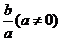 .
.
6.结论:
⑴棱锥的平行截面的性质如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比(对应角相等,对应边对应成比例的多边形是相似多边形,相似多边形面积的比等于对应边的比的平方);相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比.
⑵长方体从一个顶点出发的三条棱长分别为a,b,c,则体对角线长为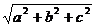
 ,全面积为2ab+2bc+2ca,体积V=abc。
,全面积为2ab+2bc+2ca,体积V=abc。
⑶正方体的棱长为a,则体对角线长为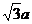 ,全面积为
,全面积为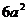 ,体积V=
,体积V=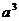 。
。
⑷球与长方体的组合体: 长方体的外接球的直径是长方体的体对角线长.
球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.
⑷正四面体的性质:设棱长为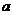 ,则正四面体的:
,则正四面体的:
①
高: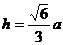 ;②对棱间距离:
;②对棱间距离: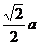 ;③内切球半径:
;③内切球半径: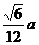 ;④外接球半径:
;④外接球半径: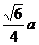 。
。
5.求距离:(步骤-------Ⅰ.找或作垂线段;Ⅱ.求距离)
点到平面的距离:①等体积法;②向量法
4.求角:(步骤-------Ⅰ.找或作角;Ⅱ.求角)
⑴异面直线所成角的求法:
①平移法:平移直线,构造三角形;②用向量法
⑵直线与平面所成的角:
①直接法(利用线面角定义);②用向量法
3.位置关系的证明(主要方法):
⑴直线与直线平行:①公理4;②线面平行的性质定理;③面面平行的性质定理。
⑵直线与平面平行:①线面平行的判定定理;②面面平行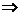 线面平行。
线面平行。
⑶平面与平面平行:①面面平行的判定定理及推论;②垂直于同一直线的两平面平行。
⑷直线与平面垂直:①直线与平面垂直的判定定理;②面面垂直的性质定理。
⑸平面与平面垂直:①定义----两平面所成二面角为直角;②面面垂直的判定定理。
注:以上理科还可用向量法。
2.表(侧)面积与体积公式:
⑴柱体:①表面积:S=S侧+2S底;②侧面积:S侧=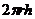 ;③体积:V=S底h
;③体积:V=S底h
⑵锥体:①表面积:S=S侧+S底;②侧面积:S侧=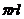 ;③体积:V=
;③体积:V=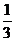 S底h:
S底h:
⑶台体:①表面积:S=S侧+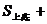 S下底;②侧面积:S侧=
S下底;②侧面积:S侧=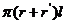 ;③体积:V=
;③体积:V=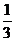 (S+
(S+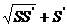 )h;
)h;
⑷球体:①表面积:S=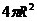 ;②体积:V=
;②体积:V=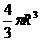 .
.
1.三视图与直观图:⑴画三视图要求:正视图与俯视图长对正;正视图与侧视图高平齐;侧视图与俯视图宽相等。 ⑵斜二测画法画水平放置几何体的直观图的要领。
11.几个公式:⑴三角形面积公式:①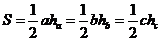 (
(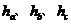 分别表示a、b、c边上的高);②
分别表示a、b、c边上的高);②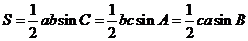 .③
.③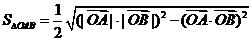
⑵内切圆半径r=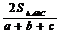 ; 外接圆直径2R=
; 外接圆直径2R=
10.正、余弦定理:
⑴正弦定理: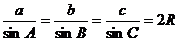 (
(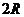 是
是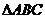 外接圆直径 )
外接圆直径 )
注:①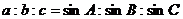 ;②
;②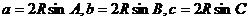 ;③
;③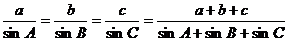 。
。
⑵余弦定理: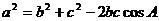 等三个;
等三个; 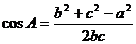 等三个。
等三个。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com