
2.复数的代数形式及其运算:设z1= a + bi , z2 = c + di (a,b,c,d∈R),则:
(1) z 1±
z2 = (a + b) ± (c + d)i;⑵ z1.z2
= (a+bi)·(c+di)=(ac-bd)+
(ad+bc)i;⑶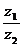 =
=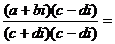
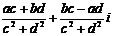 (z2≠
0) ;
(z2≠
0) ;
1.概念:
⑴z=a+bi∈R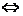 b=0 (a,b∈R)
b=0 (a,b∈R)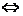 z=
z=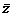
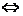 z2≥ 0;⑵z=a+bi是虚数
z2≥ 0;⑵z=a+bi是虚数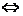 b≠ 0(a,b∈R);
b≠ 0(a,b∈R);
⑶z=a+bi是纯虚数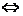 a=0且b≠ 0(a,b∈R)
a=0且b≠ 0(a,b∈R)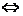 z+
z+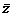 =0(z≠ 0)
=0(z≠ 0)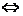 z2<0;
z2<0;
⑷a+bi=c+di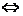 a=c且c=d(a,b,c,d∈R);
a=c且c=d(a,b,c,d∈R);
3.不等式的性质:
⑴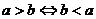 ;⑵
;⑵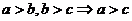 ;⑶
;⑶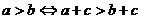 ;
;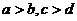
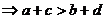 ;⑷
;⑷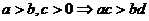 ;
;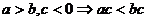 ;
;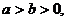
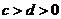
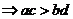 ;⑸
;⑸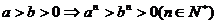 ;⑹
;⑹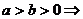
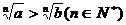
6.指数不等式与对数不等式
(1)当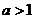 时,
时, ;
;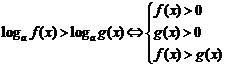 .
.
(2)当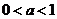 时,
时, ;
;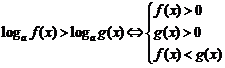
5.分式不等式:
(1)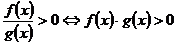 ; (2)
; (2)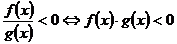 ;
;
(3)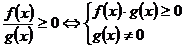 ; (4)
; (4)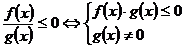 .
.
4.含有绝对值的不等式:当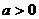 时,有:①
时,有:①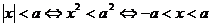 ;
;
②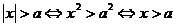 或
或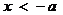 .
.
3.解一元二次不等式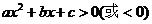 :若
:若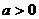 ,则对于解集不是全集或空集时,对应的
,则对于解集不是全集或空集时,对应的
解集为“大两边,小中间”.如:当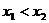 ,
,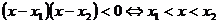 ;
;
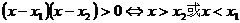 .
.
2.极值定理:已知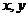 都是正数,则有:
都是正数,则有:
(1)如果积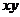 是定值
是定值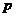 ,那么当
,那么当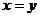 时和
时和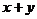 有最小值
有最小值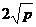 ;
;
(2)如果和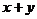 是定值
是定值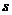 ,那么当
,那么当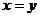 时积
时积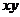 有最大值
有最大值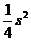 .
.
1.均值不等式:
注意:①一正二定三相等;②变形: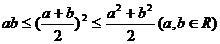 。
。
5.等差数列前n项和最值的求法:
⑴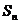 最大值
最大值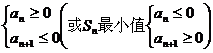 ;⑵利用二次函数的图象与性质。
;⑵利用二次函数的图象与性质。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com