
19.解(Ⅰ)由已知有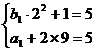 , 解得b1=1, a1=-13.
, 解得b1=1, a1=-13.
从而an =-13+(n-1)·2=2 n-15, bn=1×2 n-1=2 n-1, cn= anbn=(2n-15)2 n-1.
(Ⅱ) ∵Sn= a1b1+ a2b2+…+anbn, ①
qSn= a1b2+ a2b3+…+anbn+1. ②.
①-②得(1-q)Sn= a1b1+d( b2 +b3+…+bn)-
anbn+1= a1b1+ d·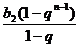 - anbn+1
- anbn+1
=-13+2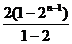 -(2n-15)2 n=-[(2n-17) 2 n+17],
-(2n-15)2 n=-[(2n-17) 2 n+17],
∴Sn=(2n-17) 2 n+17.
∴
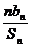 =
=
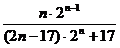 =
= =
=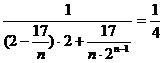
22.已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+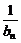 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与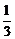 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
21.一名学生骑自行车上学,从他的家到学校的途中有6个交通岗,假设他在各交通岗遇到红灯的事件是独立的,并且概率都是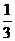 .(I)求这名学生首次遇到红灯前,已经过了两个交通岗的概率;
.(I)求这名学生首次遇到红灯前,已经过了两个交通岗的概率;
(II)求这名学生在途中遇到红灯数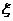 的期望与方差.
的期望与方差.
20.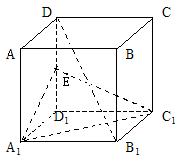 正方体
正方体 中,点E是
中,点E是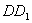 的中点,如图,
(1)求证:
的中点,如图,
(1)求证: ;
(2)求证:
;
(2)求证: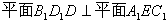 ;
(3)求证:
;
(3)求证: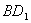 不垂直于平面
不垂直于平面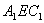 。
。
19.{an}为等差数列, 公差为d, {bn}为等比数列, 公比为q且d= q=2, b3+1= a10=5, 设cn= anbn.(Ⅰ)求数列{cn}的通项公式; (Ⅱ)设数列{cn}的前n项和为Sn,求
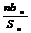 的值.
的值.
18、甲、乙两人各进行1次射击,甲击中目标的概率是0.8,乙击中目标的概率是0.7,则甲乙都击中的概率是 .0.56
17.将棱长为1的正方体木块加工成一个体积最大的球,则这个球的体积为__________,球的表面积为_________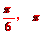
16.三棱锥S-ABC对于以下条件 ①各侧面是等腰三角形且底面是正三角形 ②底面是正三角形 ③各侧面是正三角形 ④顶点在底面的射影是底面三角形的外心.其中作为三棱锥S-ABC构成正三棱锥的必要不充分条件的是 . (1)(2) (4)
15、某保险公司新开设了一项保险业务,若在一年内事件E发生,该公司要赔偿a元.设在一年内E发生的概率为p,为使公司收益的期望值等于a的百分之十,公司应要求顾客交 保险金。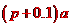
14.用数学归纳法证明:“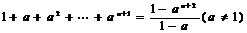 ”在验证
”在验证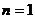 时,左端计算所得的项为C
时,左端计算所得的项为C
A 1 B 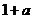 C
C 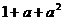 D
D 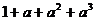
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com