
22.已知数列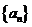 满足
满足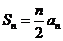 (n∈N*),
(n∈N*),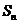 是
是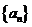 的前n项的和,并且
的前n项的和,并且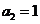 .(1)求数列
.(1)求数列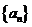 的前
的前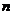 项的和;
项的和;
(2)证明: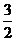 ≤
≤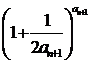
 .
.
19解 假设存在a、b、c使题设的等式成立,
假设存在a、b、c使题设的等式成立,
这时令n=1,2,3,有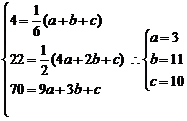
于是,对n=1,2,3下面等式成立
1·22+2·32+…+n(n+1)2=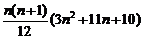
记Sn=1·22+2·32+…+n(n+1)2
设n=k时上式成立,即Sk=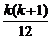 (3k2+11k+10)
(3k2+11k+10)
那么Sk+1=Sk+(k+1)(k+2)2= (k+2)(3k+5)+(k+1)(k+2)2
(k+2)(3k+5)+(k+1)(k+2)2
=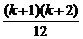 (3k2+5k+12k+24)
(3k2+5k+12k+24)
=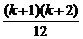 [3(k+1)2+11(k+1)+10]
[3(k+1)2+11(k+1)+10]
也就是说,等式对n=k+1也成立
综上所述,当a=3,b=11,c=10时,题设对一切自然数n均成立
21. 对5副不同的手套进行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只.(Ⅰ)求下列事件的概率:①A:甲正好取得两只配对手套; ②B:乙正好取得两只配对手套;(Ⅱ)A与B是否独立?并证明你的结论.
20.如图, 正方体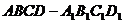 的棱长为1, 点
的棱长为1, 点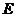 是棱
是棱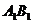 的中点,
的中点,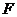 是棱
是棱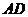 的中点.
的中点.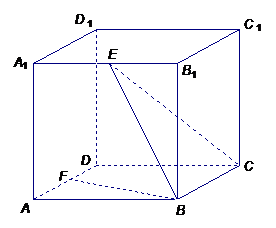 (Ⅰ) 求证:
(Ⅰ) 求证: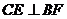 ;
;
(Ⅱ)
求点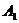 到平面
到平面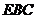 的距离.
的距离.
19.是否存在a、b、c使得等式1·22+2·32+…+n(n+1)2= (an2+bn+c)
(an2+bn+c)
18.已知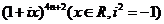 展开式中的实数关于x的多项式,则此多项式系数和为 . 0
展开式中的实数关于x的多项式,则此多项式系数和为 . 0
17.两腰长均是1的等腰Rt△ABC1和等腰Rt△ABC2所在平面成60°的二面角,则两点C1与C2的距离是
.(写出所有可能的值) 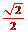 , 1,
, 1, 
16.已知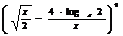 的展开式中
的展开式中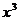 的系数为
的系数为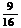 ,则实数
,则实数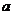 的值为 1/16
的值为 1/16
15.四面体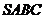 的三组对棱分别相等,且依次为
的三组对棱分别相等,且依次为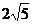 ,
,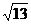 ,
,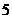 ,则此四面体的体积是 8
,则此四面体的体积是 8
14.若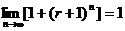 ,则实数
,则实数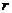 的取值范围是
。(-2, 0)
的取值范围是
。(-2, 0)
13.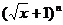 的展开式中,只有第六项的系数最大,则
的展开式中,只有第六项的系数最大,则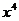 的系数是
. 45
的系数是
. 45
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com