
根据近年来化学高考试题中有关化学实验内容的题目分析,下列内容是化学实验部分考查的重点:
l.实验基本操作和技能
这类试题的特点通常是给出限定的仪器、药品和一些操作步骤,要求正确完成某项实验操作,既有常见仪器的使用方法,又有基本操作的正误辨别,着重考查考生对中学化学实验基本操作技能掌握的情况,题目的难度不高,但并不容易得满分。
2.正确运用实验原理和正确认识实验装置
这类试题通常是给出限定的实验装置、反应条件、实验现象和有关数据,要求考生根据实验原理及试题中所给予的信息,结合元素化合物知识,选用仪器药品,正确认识、选择装置,说明装置中某些仪器的作用,描述实验现象,写有关化方程式,进行数据分析.指出实验中必须注意的某些问题等等,主要考查考生的观察能力与分析综合及评价的能力。这类题目具有一定的综合性,具有较大的区分度。
22.已知椭圆C1: ,抛物线C2:
,抛物线C2: ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.
(1)当AB⊥ 轴时,求
轴时,求 、
、 的值,并判断抛物线C2的焦点是否在直线AB上;
的值,并判断抛物线C2的焦点是否在直线AB上;
(2)是否存在 、
、 的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的
的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的 、
、 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
2007-2008学年度南昌市高三第一轮复习训练题
21. 已知椭圆 ,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线
,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线 于点N,且
于点N,且 .
.
(1)求椭圆的离心率;
(2)若斜率为1的直线l交椭圆于P、Q两点,求证: 与向量
与向量 =(-3,1)共线(其中O为坐标原点)
=(-3,1)共线(其中O为坐标原点)
20.(理)已知动点M到点F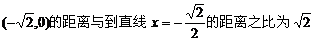 .
.
(1)求动点M的轨迹C的方程;
(2)若过点E(0,1)的直线与曲线C在y轴左侧交于不同的两点A、B,点P(-2,0)满足 ,求直线PN在y轴上的截距d的取值范围..
,求直线PN在y轴上的截距d的取值范围..
(文)直线l: 与曲线
与曲线 的左支交于不同的两点A、B,直线m过点P(-2,0)和AB的中点M,求m在y轴上截距b的取值范围.
的左支交于不同的两点A、B,直线m过点P(-2,0)和AB的中点M,求m在y轴上截距b的取值范围.
19. 已知椭圆
已知椭圆 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(1)求过点O、F,并且与椭圆的左准线 相切的圆的方程;
相切的圆的方程;
(2)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,
线段AB的垂直平分线与 轴交于点G,求点G横坐标的取值范围。
轴交于点G,求点G横坐标的取值范围。
17. 过抛物线
过抛物线 的焦点作一条斜率为k(k≠0)的弦,此弦满足:①弦长不超过8;②弦所在的直线与椭圆3x2 + 2y2
= 2相交,求k的取值范围.
的焦点作一条斜率为k(k≠0)的弦,此弦满足:①弦长不超过8;②弦所在的直线与椭圆3x2 + 2y2
= 2相交,求k的取值范围.




 18.若点P在椭圆
18.若点P在椭圆 上,设
上,设 ,(1)试用m表示
,(1)试用m表示 ;
;
(2)在(1)的条件下,求 的最大值和最小值
的最大值和最小值
16. 已知抛物线 的直线与抛物线相交于
的直线与抛物线相交于 两点,则
两点,则 的最小值是___________
的最小值是___________
15.若椭圆 的一条准线方程为
的一条准线方程为 ,则
,则 ;此时,定点
;此时,定点 与椭圆C上动点距离的最小值为
.
与椭圆C上动点距离的最小值为
.
14. 与双曲线 有共同的渐近线,且经过点
有共同的渐近线,且经过点 的双曲线的一个焦点到一条渐近线的距离等于
的双曲线的一个焦点到一条渐近线的距离等于
13. 已知点P(x,y)是抛物线y2=x上任意一点,且点P在直线 的上方,则实数a的取值范围为
.
的上方,则实数a的取值范围为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com