
右图是“我国某地区气象灾害成因示意图”,读图完成3-4题。
3.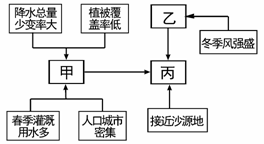 图中甲、乙、丙气象灾害分别是
图中甲、乙、丙气象灾害分别是
A.春旱、寒潮、沙尘暴
B.寒潮、台风、沙尘暴
C.伏旱、暴雪、沙尘暴
D.伏旱、洪涝、冻害
4.该地区最有可能是
A.青藏高原 B.东北平原
C.华北平原 D.东南丘陵
2.下列全球变暖对人类活动影响的叙述,正确的是
A.有利于航海事业的发展
B.会抑制疾病的发病率
C.对海洋生态系统影响很小
D.将使世界干旱、半干旱地区的土地荒漠化问题更加突出
1.读下图,图中“*”表示人口年龄构成状况,其中0-14岁人口的比重约是
A.93% B.23%
C.13% D.60%
4.进位值
我们常见的数字都是十进制数,比如一般的数值计算,但是并不是生活中的每一种数字都是十进制的。比如时间和角度的单位是六十进制,电子计算机的指令用的是二进制,早先的计算机的用的是十六进制的。
3.排序
(1)直接插入排序
插入排序的思想就是读一个,排一个。将数组的第1个数据放入数组的第1个位置,以后读入的数据与已存入数组的数据进行比较,确定它按从大到小(从小到大)的排列中排在正确的位置。将该位置以及以后的元素向后推移一个位置,将读入的新数填到空出的位置即可。
(2)冒泡排序
以从大到小为例:依次比较相邻的两个数,把大的放前面,小的放后面。即首先比较第1个数和第2个数,大数放前,小数放后;然后比较完成第2个数和第3个数;......;直到比较完了最后两个数。第一趟排序结束,最小的一定沉到最后。重复上过程,仍从第1个数开始,到最后第2个数...... 由于在排序过程中总是大数往前,小数往后,相当气泡上升,所以叫冒泡排序。
2.我们以这个5次多项式函数为例加以说明,设:
f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0
首先,让我们以5次多项式一步步地进行改写:
f(x)=(a5x4+a4x3+a3x2+a2x+a1)x+a0
=((a5x3+a4x2+ a3x+a2)x+a1)x+a0
=(((a5x2+a4x+ a3)x+a2)x+a1)x+a0
=((((a5x+a4)x+ a3)x+a2)x+a1)x+a0
上面的分层计算。只用了小括号,计算时,首先计算最内层的括号,然后由里向外逐层计算,直到最外层的括号,然后加上常数项即可。

1.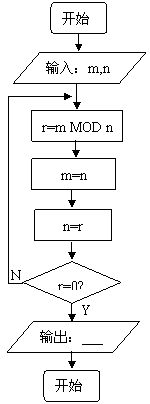 求最大公约数
求最大公约数
(1)辗转相除法
程序框图与程序语句
程序:
INPUT “m,n=”;m,n
DO
r=m MOD n
m=n
n=r
LOOP UNTIL r=0
END
(2)更相减损术
更相减损术程序:
INPUT “请输入两个不相等的正整数”;a,b
i=0
WHILE a MOD 2=0 AND b MOD 2=0
a=a/2
b=b/2
i=i+1
WEND
DO
IF b<a THEN
t=a
a=b
b=t
END IF
c=a-b
a=b
b=c
LOOP UNTIL a=b
PRINT a^i
END
对于两个正整数如何选择合适的方法求他们的最大公约数
|
方法 |
适用范围及特点 |
|
短除法 |
适合两个较小的正整数或两个质因数较少的正整数,简便易操作。 |
|
穷举法 |
适合计算机操作,但一一验证过于繁琐。 |
|
辗转相除法 |
适用于两个较大的正整数,以除法为主,辗转相除法计算次数相对较少,特别当两个数字大小差别较大时计算次数较明显。 |
|
更相减损术 |
适用于两个较大的正整数,更相减损术以减法为主,计算次数上相对于辗转相处法较多。 |
6] -3 0 15
[-3 6] 0 15
[-3 0 6] 15
[-3 0 6 15]
用冒泡排序法排序:
|
6 |
|
6 |
|
6 |
|
6 |
|
6 |
|
6 |
|
6 |
|
15 |
|
15 |
|
15 |
|
-3 |
|
-3 |
|
0 |
|
0 |
|
0 |
|
15 |
|
15 |
|
6 |
|
6 |
|
6 |
|
0 |
|
0 |
|
-3 |
|
15 |
|
15 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
15 |
|
15 |
|
15 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
|
-3 |
题型4:进位值
例7.把十进制数89化为三进制数,并写出程序语句.
解析:具体的计算方法如下:
89=3×29+2
29=3×9+2
9=3×3+0
3=3×1+0
1=3×0+1
所以:89(10)=1011001(3)。
点评:根据三进制数满三进一的原则,可以用3连续去除89及其所的得的商,然后按倒序的先后顺序取出余数组成数据即可。
例8.将8进制数314706(8)化为十进制数,并编写出一个实现算法的程序。
解析:314706(8)=3×85+1×84+4×83+7×82+0×81+6×80=104902。
所以,化为十进制数是104902。
点评:利用把k进制数转化为十进制数的一般方法就可以把8进制数314706(8)化为十进制数,然后根据该算法,利用GET函数,应用循环结构可以设计程序。
题型1:求最大公约数
例1.(1)用辗转相除法求123和48的最大公约数?
(2)用更相减损来求80和36的最大公约数?
解析:(1)辗转相除法求最大公约数的过程如下:(建立带余除式)
123=2×48+27
48=1×27+21
27=1×21+6
21=3×6+3
6=2×3+0
最后6能被3整除,得123和48的最大公约数为3。
(2)分析:我们将80作为大数,36作为小数,执行更相减损术来求两数的最大公约数。执行结束的准则是减数和差相等。
更相减损术:
因为80和36都是偶数,要去公因数2。
80÷2=40,36÷2=18;
40和18都是偶数,要去公因数2。
40÷2=20,18÷2=9
下面来求20与9的最大公约数,
20-9=11
11-9=2
9-2=7
7-2=5
5-2=3
3-2=1
2-1=1
可得80和36的最大公约数为22×1=4。
点评:对比两种方法控制好算法的结束,辗转相除法是到达余数为0,更相减损术是到达减数和差相等。
例2.设计一个算法,求出840与1764的最大公因数。
解析:我们已经学习过了对自然数的素因数分解的方法,下面的算法就是在此基础上设计的。
解题思路如下:
首先对两个数进行素因数分解:
840=23×3×5×7,1764=22×32×72,
其次,确定两个数的公共素因数:2,3,7。
接着确定公共素因数的指数:对于公共素因数2,840中为23,1764中为22,应取较少的一个22,同理可得下面的因数为3和7。
算法步骤:
第一步:将840进行素数分解23×3×5×7;
第二步:将1764进行素数分解22×32×72;
第三步:确定它们的公共素因数:2,3,7;
第四步:确定公共素因数2,3,7的指数分别是:2,1,1;
第五步:最大公因数为22×31×71=84。
点评:质数是除1以外只能被1和本身整除的正整数,它应该是无限多个,但是目前没有一个规律来确定所有的质数。
题型2:秦九韶算法
例3.(2005北京,14)已知n次多项式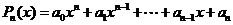 ,如果在一种算法中,计算
,如果在一种算法中,计算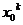 (k=2,3,4,…,n)的值需要k-1次乘法,计算
(k=2,3,4,…,n)的值需要k-1次乘法,计算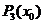 的值共需要9次运算(6次乘法,3次加法),那么计算
的值共需要9次运算(6次乘法,3次加法),那么计算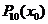 的值共需要
次运算。下面给出一种减少运算次数的算法:
的值共需要
次运算。下面给出一种减少运算次数的算法: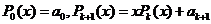 (k=0, 1,2,…,n-1).利用该算法,计算
(k=0, 1,2,…,n-1).利用该算法,计算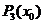 的值共需要6次运算,计算
的值共需要6次运算,计算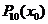 的值共需要
次运算。
的值共需要
次运算。
答案:65;20。
点评:秦九韶算法适用一般的多项式f(x)=anxn+an-1xn-1+….+a1x+a0的求值问题。直接法乘法运算的次数最多可到达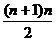 ,加法最多n次。秦九韶算法通过转化把乘法运算的次数减少到最多n次,加法最多n次。
,加法最多n次。秦九韶算法通过转化把乘法运算的次数减少到最多n次,加法最多n次。
例4.已知多项式函数f(x)=2x5-5x4-4x3+3x2-6x+7,求当x=5时的函数的值。
解析:把多项式变形为:f(x)= 2x5-5x4-4x3+3x2-6x+7
=((((2x-5)x-4)x+3)x-6)x+7
计算的过程可以列表表示为:
|
多项式x系数 |
2 |
-5 |
-4 |
3 |
-6 |
7 |
运算 |
|
|
运算所得的值 |
|
 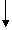 10 10 |
 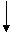 25 25 |
 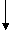 105 105 |
 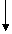 540 540 |
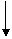 2670 2670 |
+ |
|
|
变形后x的"系数" |
2 |
5 |
21 |
108 |
534 |
2677 |
*5 |
最后的系数2677即为所求的值。
算法过程:
v0=2
v1=2×5-5=5
v2=5×5-4=21
v3=21×5+3=108
v4=108×5-6=534
v5=534×5+7=2677
点评:如果多项式函数中有缺项的话,要以系数为0的项补齐后再计算。
题型三:排序
例4.试用两种排序方法将以下8个数:7,1,3,12,8,4,9,10。按照从大到小的顺序进行排序。
解析:可以按照直接插入排序和冒泡排序这两种方法的要求,结合图形,分析写出。
直接插入法排序:
7] 1 3 12 8 4 9 10
[7 1] 3 12 8 4 9 10
[7 3 1] 12 8 4 9 10
[12 7 3 1] 8 4 9 10
[12 8 7 3 1] 4 9 10
[12 8 7 4 3 1] 9 10
[12 9 8 7 4 3 1] 10
[12 10 9 8 7 4 3 1]
冒泡排序
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
7 |
|
1 |
1 |
3 |
|
3 |
|
3 |
|
3 |
|
3 |
|
3 |
||
|
3 |
3 |
1 |
|
12 |
|
12 |
|
12 |
|
12 |
|
12 |
||
|
12 |
12 |
12 |
|
1 |
|
8 |
|
8 |
|
8 |
|
8 |
||
|
8 |
8 |
8 |
|
8 |
|
1 |
|
4 |
|
4 |
|
4 |
||
|
4 |
4 |
4 |
|
4 |
|
4 |
|
1 |
|
9 |
|
9 |
||
|
9 |
9 |
9 |
|
9 |
|
9 |
|
9 |
|
1 |
|
10 |
||
|
10 |
10 |
10 |
|
10 |
|
10 |
|
10 |
|
10 |
|
|
第一趟
|
7 |
|
7 |
|
12 |
|
12 |
|
12 |
|
12 |
|
3 |
|
12 |
|
8 |
|
8 |
|
9 |
|
10 |
|
12 |
|
8 |
|
7 |
|
9 |
|
10 |
|
9 |
|
8 |
|
4 |
|
9 |
|
10 |
|
8 |
|
8 |
|
4 |
|
9 |
|
10 |
|
7 |
|
7 |
|
7 |
|
9 |
|
10 |
|
4 |
|
4 |
|
4 |
|
4 |
|
10 |
|
3 |
|
3 |
|
3 |
|
3 |
|
3 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
|
1 |
第2趟 第3趟 第4趟 第5趟 第6趟
点评:直接插入法和冒泡法排序是常见的排序方法,通过该例,我们对比可以发现,直接插入排序比冒泡排序更有效一些,执行的操作步骤更少一些。
例6.给出以下四个数:6,-3,0,15,用直接插入法排序将它们按从小到大的顺序排列,用冒泡法将它们按从大到小的顺序排列。
分析:不论从大到小的顺序还是按从大到小的顺序,都可按两种方法的步骤进行排序。
解析:
直接插入排序法:
4.进位制
(1)概念
进位制是一种记数方式,用有限的数字在不同的位置表示不同的数值。可使用数字符号的个数称为基数,基数为n,即可称n进位制,简称n进制。现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数。
对于任何一个数,我们可以用不同的进位制来表示。比如:十进数57,可以用二进制表示为111001,也可以用八进制表示为71、用十六进制表示为39,它们所代表的数值都是一样的。
一般地,若k是一个大于一的整数,那么以k为基数的k进制可以表示为:
 ,
,
而表示各种进位制数一般在数字右下脚加注来表示,如111001(2)表示二进制数,34(5)表示5进制数。
(2)进位制间的转换
关于进位制的转换,教科书上以十进制和二进制之间的转换为例讲解,并推广到十进制和其它进制之间的转换。这样做的原因是,计算机是以二进制的形式进行存储和计算数据的,而一般我们传输给计算机的数据是十进制数据,因此计算机必须先将十进制数转换为二进制数,再处理,显然运算后首次得到的结果为二进制数,同时计算机又把运算结果由二进制数转换成十进制数输出。
非十进制数转换为十进制数比较简单,只要计算下面的式子值即可:

第一步:从左到右依次取出k进制数 各位上的数字,乘以相应的k的幂,k的幂从n开始取值,每次递减1,递减到0,即
各位上的数字,乘以相应的k的幂,k的幂从n开始取值,每次递减1,递减到0,即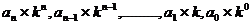 ;
;
第二步:把所得到的乘积加起来,所得的结果就是相应的十进制数。
十进制数转换成非十进制数
把十进制数转换为二进制数,教科书上提供了“除2取余法”,我们可以类比得到十进制数转换成k进制数的算法“除k取余法”。
非十进制之间的转换
一个自然的想法是利用十进制作为桥梁。教科书上提供了一个二进制数据与16进制数据之间的互化的方法,也就是先有二进制数转化为十进制数,再由十进制数转化成为16进制数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com