

13. 证明: 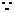 四边形
四边形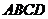 和四边形
和四边形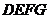 都是正方形
都是正方形
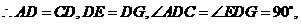
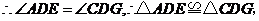
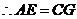
12.证明:(1)在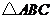 和
和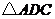 中
中
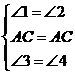
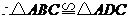 .
.
(2)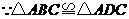 ,
,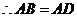 .又
.又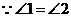 ,
,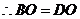 .
.
11.
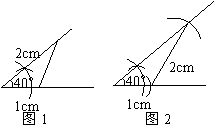
解:(1)如图1;
(2)如图2;
(3)4. (8分)

10. 证明: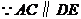 ,
,
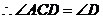 ,
,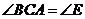 .、)
.、)
又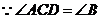 ,
,
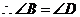 .
.
又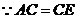 ,
,
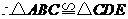 . (6分
. (6分
9. 证明: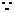 AC∥DE, BC∥EF
AC∥DE, BC∥EF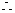
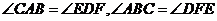 ,又
,又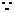 AC=DE
AC=DE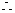
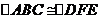 , ∴AB=DF ∴AF=BD
, ∴AB=DF ∴AF=BD
8. 证明:(1)①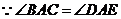
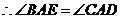
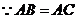 ,
,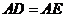
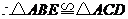
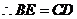 ·················································································································· 3分
·················································································································· 3分
②由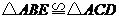 得
得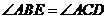 ,
,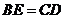
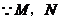 分别是
分别是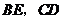 的中点,
的中点,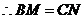 ························································· 4分
························································· 4分
又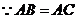
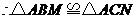
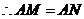 ,即
,即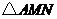 为等腰三角形······································································ 6分
为等腰三角形······································································ 6分
(2)(1)中的两个结论仍然成立.············································································· 8分
(3)在图②中正确画出线段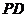
由(1)同理可证
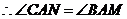
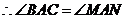
又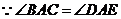
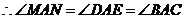
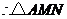 ,
,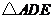 和
和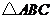 都是顶角相等的等腰三角形······································· 10分
都是顶角相等的等腰三角形······································· 10分
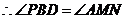 ,
,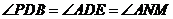
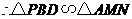 12分
12分
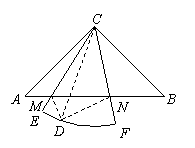
7. (Ⅰ)证明 将△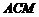 沿直线
沿直线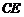 对折,得△
对折,得△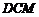 ,连
,连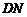 ,
,
则△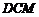 ≌△
≌△ . ························································································· 1分
. ························································································· 1分
 有
有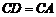 ,
, ,
,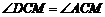 ,
,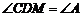 .
.
又由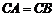 ,得
,得 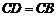 . ········································· 2分
. ········································· 2分
由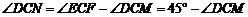 ,
,
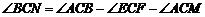
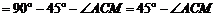 ,
,
得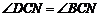 . ··································································································· 3分
. ··································································································· 3分
又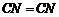 ,
,
∴△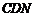 ≌△
≌△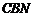 . ···························································································· 4分
. ···························································································· 4分
有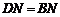 ,
,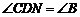 .
.
∴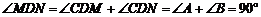 .····························································· 5分
.····························································· 5分
∴在Rt△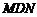 中,由勾股定理,
中,由勾股定理,
得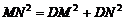 .即
.即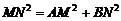 . ························································ 6分
. ························································ 6分
(Ⅱ)关系式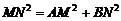 仍然成立. ····························································· 7分
仍然成立. ····························································· 7分
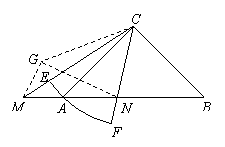 证明 将△
证明 将△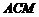 沿直线
沿直线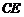 对折,得△
对折,得△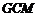 ,连
,连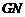 ,
,
则△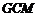 ≌△
≌△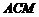 . ···················································· 8分
. ···················································· 8分
有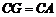 ,
,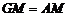 ,
,
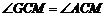 ,
,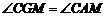 .
.
又由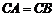 ,得
,得 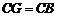 .
.
由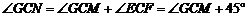 ,
,
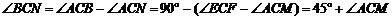 .
.
得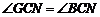 . ································································································ 9分
. ································································································ 9分
又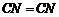 ,
,
∴△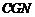 ≌△
≌△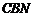 .
.
有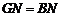 ,
,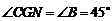 ,
,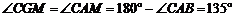 ,
,
∴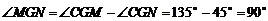 .
.
∴在Rt△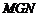 中,由勾股定理,
中,由勾股定理,
得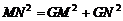 .即
.即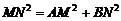 .························································ 10分
.························································ 10分
6. 解:(1)证明: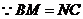 ,
,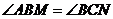 ,
,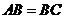 ,
,
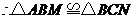 ,
,
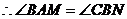 ,
,
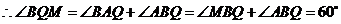 .
.
(2)①是;②是;③否.
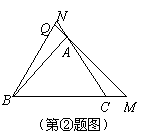 ②的证明:如图,
②的证明:如图,
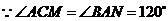 ,
,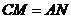 ,
,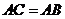 ,
,
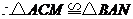 ,
,
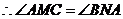 ,
,
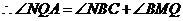
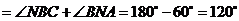 ,
,
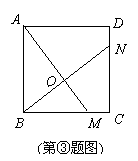
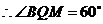 .
.
③的证明:如图,
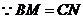 ,
,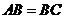 ,
,
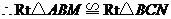 ,
,
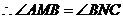 .又
.又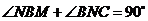 ,
,
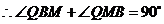 ,
,
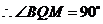 ,即
,即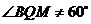 .
.
5. 解:⑴证明:∵AC平分∠MAN,∠MAN=120°,
∴∠CAB=∠CAD=60°,
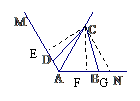 ∵∠ABC=∠ADC=90°,
∵∠ABC=∠ADC=90°,
∴∠ACB=∠ACD=30°,…………1分
∴AB=AD=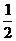 AC,……………………2分
AC,……………………2分
∴AB+AD=AC。……………………3分
⑵成立。……………………………r…4分
证法一:如图,过点C分别作AM、AN的垂线,垂足分别为E、F。
∵AC平分∠MAN,∴CE=CF.
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC,………………………………………………………………5分
∵∠CED=∠CFB=90°,∴△CED≌△CFB,∴ED=FB,……………………6分
∴AB+AD=AF+BF+AE-ED=AF+AE,由⑴知AF+AE=AC,
∴AB+AD=AC……………………………………………………………………7分
证法二:如图,在AN上截取AG=AC,连接CG.
∵∠CAB=60°,AG=AC,∴∠AGC=60°,CG=AC=AG,…………5分
∵∠ABC+∠ADC=180°,∠ABC+∠CBG=180°,
∴∠CBG=∠ADC,∴△CBG≌△CDA,……………………………………6分
∴BG=AD,
∴AB+AD=AB+BG=AG=AC,…………………………………………7分
⑶①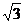 ;………………………………………………………………………8分
;………………………………………………………………………8分
②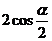 .………………………………………………………………………9分
.………………………………………………………………………9分
证明:由⑵知,ED=BF,AE=AF,
在Rt△AFC中,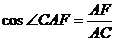 ,即
,即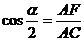 ,
,
∴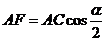 ,………………………………………………………………10分
,………………………………………………………………10分
∴AB+AD=AF+BF+AE-ED=AF+AE=2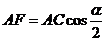 ,…………11分
,…………11分
4. 证明:(1)证明:方法一:在△ACD和△BCE中,
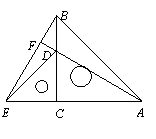 AC=BC,
AC=BC,
∠DCA=∠ECB=90°,
DC=EC,
∴ △ACD≌△BCE(SAS). ………………2分
∴ ∠DAC=∠EBC. ………………………3分
∵ ∠ADC=∠BDF,
∴ ∠EBC+∠BDF=∠DAC+∠ADC=90°.
∴ ∠BFD=90°.
∴ AF⊥BE. …………………………………5分
方法二:∵ AC=BC,DC=EC,
 ∴
∴ 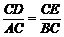 .即tan∠DAC=tan∠EBC.
.即tan∠DAC=tan∠EBC.
∴ ∠DAC=∠EBC.(下略)…………………3分
(2)AF⊥BE. …………………………………6分
∵ ∠ABC=∠DEC=30°,∠ACB=∠DCE=90°,
∴ 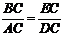 =tan60°. ……………………7分
=tan60°. ……………………7分
∴ △DCA∽△ECB. …………………………8分
∴ ∠DAC=∠EBC. …………………………9分
∵ ∠ADC=∠BDF,
∴ ∠EBC+∠BDF=∠DAC+∠ADC=90°.
∴ ∠BFD=90°.
∴ AF⊥BE. ……………………………………………………………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com