
2. 已知点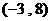 在反比例函数
在反比例函数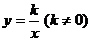 的图象上,那么下列各点中在此函数图象上的是( )
的图象上,那么下列各点中在此函数图象上的是( )
A. 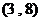 B.
B. 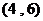 C.
C. 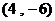 D.
D. 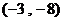
1. 在函数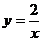 ,
,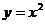 和
和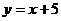 的图象中,是中心对称图形,且对称中心是原点的图象共有( )
的图象中,是中心对称图形,且对称中心是原点的图象共有( )
A. 0个 B. 1个 C. 2个 D. 3个
⒗(本小题满分12分)在直角坐标系中,已知 ,
,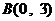 ,
,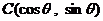 .
.
⑴若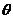 锐角,且
锐角,且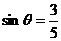 ,求
,求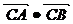 ;
;
⑵若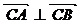 ,求
,求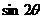 .
.
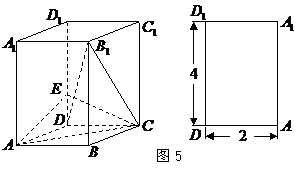 ⒘(本小题满分13分)如图5,已知正四棱柱
⒘(本小题满分13分)如图5,已知正四棱柱 与它的侧视图(或称左视图),
与它的侧视图(或称左视图), 是
是 上一点,
上一点,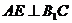 .
.
⑴求证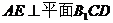 ;
;
⑵求三棱锥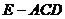 的体积.
的体积.
⒙(本小题满分13分)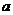 、
、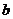 是常数,关于
是常数,关于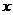 的一元二次方程
的一元二次方程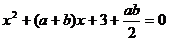 有实数解记为事件
有实数解记为事件 .
.
⑴若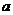 、
、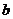 分别表示投掷两枚均匀骰子出现的点数,求
分别表示投掷两枚均匀骰子出现的点数,求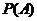 ;
;
⑵若 、
、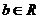 ,
,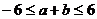 且
且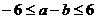 ,求
,求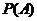 .
.
⒚(本小题满分14分)已知圆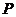 :
: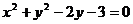 ,抛物线
,抛物线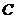 以圆心
以圆心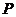 为焦点,以坐标原点为顶点.
为焦点,以坐标原点为顶点.
⑴求抛物线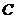 的方程;
的方程;
⑵设圆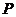 与抛物线
与抛物线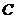 在第一象限的交点为
在第一象限的交点为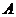 ,过
,过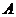 作抛物线
作抛物线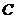 的切线与
的切线与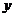 轴的交点为
轴的交点为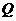 ,动点
,动点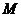 到
到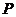 、
、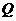 两点距离之和等于
两点距离之和等于 ,求
,求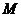 的轨迹方程.
的轨迹方程.
⒛(本小题满分14分)已知函数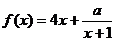 ,
,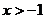 ,
,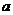 是常数.
是常数.
⑴若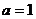 ,试证明
,试证明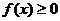 ;
;
⑵若对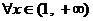 ,
,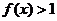 恒成立,求常数
恒成立,求常数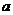 的取值范围.
的取值范围.
21.(本小题满分14分)设数列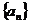 的前
的前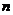 (
(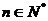 )项和为
)项和为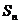 ,
,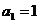 ,
,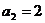 ,当
,当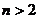 时,
时,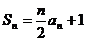 .
.
⑴求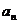 ;
;
⑵求数列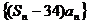 (
(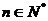 )最小的项.
)最小的项.
贵州省晴隆一中2009年高中毕业班强化训练
㈠必做题(11-13题)
 ⒒已知数列
⒒已知数列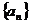 ,
, ,则
,则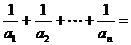 .
.
⒓双曲线的一个焦点是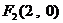 ,离心率
,离心率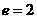 ,则
,则
双曲线的标准方程是 .
⒔定义在实数集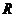 上的函数
上的函数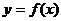 ,其对应关系
,其对应关系
由程序框图(如图3)给出,则 ,
,
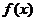 的解析式是 .
的解析式是 .
㈡选做题(14-15题,考生只能从中选做一题)
⒕(坐标系与参数方程选做题)在平面直角坐标系 中,
中,
曲线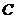 的参数方程为
的参数方程为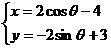 (参数
(参数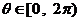 ).则曲线
).则曲线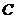 的普通方程
的普通方程
是
,曲线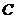 上的点到坐标原点距离的最小值是
.
上的点到坐标原点距离的最小值是
.
 ⒖(几何证明选讲选做题)如图4,
⒖(几何证明选讲选做题)如图4, 是圆
是圆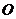 的内接等边
的内接等边
三角形,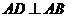 ,与
,与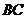 的延长线相交于
的延长线相交于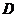 ,与圆
,与圆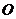
相交于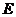 .若圆
.若圆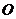 的半径
的半径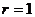 ,则
,则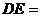 .
.
⒈设集合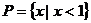 ,集合
,集合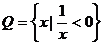 ,则
,则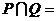
A.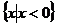 B.
B.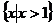 C.
C.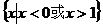 D.空集
D.空集
⒉若复数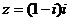 (
(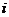 为虚数单位),则
为虚数单位),则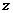 的共轭复数
的共轭复数
A.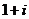 B.
B.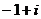 C.
C.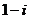 D.
D.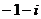
⒊已知命题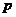 :
: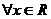 ,
,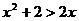 .则它的否定是
.则它的否定是
A. :
: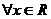 ,
,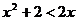 B.
B. :
: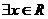 ,
,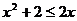
C. :
: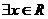 ,
,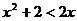 D.
D. :
: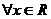 ,
,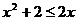
⒋已知函数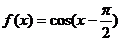 ,
,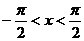 .则函数
.则函数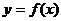 是
是
A.单调递增的奇函数 B.单调递增的偶函数
C.单调递减的奇函数 D.单调递减的偶函数
 ⒌已知向量
⒌已知向量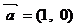 ,向量
,向量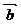 与
与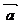 的夹角为
的夹角为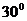 ,且
,且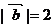 .则
.则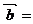
A.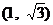 B.
B.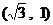 C.
C.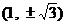 D.
D.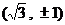
⒍已知某几何体是一个圆柱和一个球的组合体,球的直径和
圆柱底面直径相等,它的正视图(或称主视图)如图1所示.
这个几何体的表面积是
A.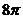 B.
B.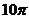 C.
C.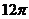 D.
D.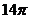
⒎若曲线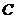 :
: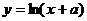 (
(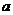 是常数)经过原点
是常数)经过原点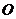 ,则曲线
,则曲线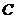 在
在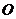 点的切线是
点的切线是
A.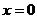 B.
B.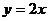 C.
C.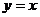 D.
D.
⒏随机调查某校50个学生在“六一”儿童节的午餐费,结果如下表:
|
餐费(元) |
3 |
4 |
5 |
|
人数 |
10 |
20 |
20 |
这50个学生“六一”节午餐费的平均值和方差分别是
A.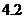 ,
, B.
B.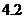 ,
,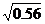 C.
C.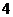 ,
, D.
D.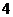 ,
,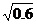
⒐在平面直角坐标系 中,已知点
中,已知点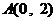 、
、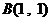 ,直线
,直线
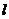 经过点
经过点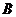 且与线段
且与线段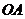 相交.则直线
相交.则直线
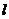 倾斜角
倾斜角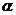 的取值范围是
的取值范围是
A.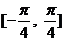 B.
B. 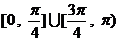 C.
C.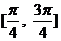 D.
D.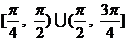
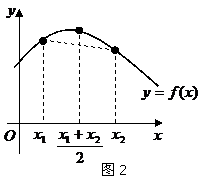 ⒑若对
⒑若对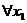 、
、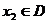 ,都有
,都有 ,则称区间
,则称区间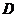 为函数
为函数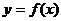 的一个凸区间(如图2).在下列函数中,
的一个凸区间(如图2).在下列函数中,
①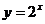 ;②
;②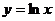 ;③
;③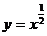 ;④
;④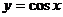
以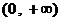 为一个凸区间的函数有:
为一个凸区间的函数有:
A.  个
B.
个
B. 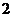 个
个
C. 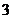 个 D.
个 D. 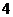 个
个
☆竖直上抛运动的实例分析
[例题]某人在高层楼房的阳台外侧以2 0 m/s的速度竖直向上抛出一个石块,石块运动到离抛出点15m处时,所经历的时间为多少?
(不计空气阻力,取g =10m/s2)
分析:石块运动到离抛出点15m处时,石块的位置是在抛出点上方还是在抛出点下方?如果是在抛出点上方的话,是处于上升阶段还是处于下降阶段?
从题意来看,石块抛出后能够上升的最大高度为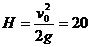 m>15m。
m>15m。
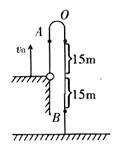
这样石块运动到离抛出点15 m处的位置必定有两个,如图所示,因而所经历的时间必为三个。
分段法:
石块上升到最高点所用的时间为:
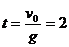 s
s
2 s前石块第一次通过“离抛出点15 m处”;2 s时石块到达最高点,速度变为零,随后石块开始做自由落体运动,会第二次经过“离抛出点15 m处”;当石块落到抛出点下方时,会第三次经过“离抛出点15m处”。这样此题应有三解。
当石块在抛出点上方距抛出点15m处时取向上为正方向,则位移x = +15m,a= - g = - 10 m/s2 ,代入公式
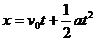
得: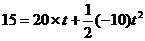
解得 t1=1 s;t2=3 s
t1=1 s对应着石块上升时到达“离抛出点15 m处”时所用的时间,而t2=3 s则对应着从最高点往回落时第二次经过“离抛出点15 m处”时所用的时间。
由于石块上升的最大高度H=20m,所以,石块落到抛出点下方“离抛出点15m处”时,自由下落的总高度为HOB=20m+15m=35m,下落此段距离所用的时间
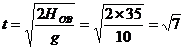 s
s
石块从抛出到第三次经过“离抛出点15m处”时所用的时间为:t3=2 s+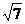 s=(2+
s=(2+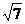 )s
)s
★课余作业
复习全章内容,准备章节测验。
★教学体会
思维方法是解决问题的灵魂,是物理教学的根本;亲自实践参与知识的发现过程是培养学生能力的关键,离开了思维方法和实践活动,物理教学就成了无源之水、无本之木。学生素质的培养就成了镜中花,水中月。
通过这节课的学习,我们从伽利略对落体的研究上,学习他的观察思考等科学方法,为我们下一步(以后)的探究打下基础,不能盲目,也不能怕困难,要用科学的方法指导我们。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com