
1.(1)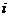 -1
-1 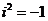
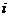 -1
-1 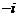 1 (2)
1 (2)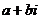 实数 虚部 纯虚数
实数 虚部 纯虚数
(3)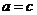 且
且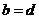
2. 假设当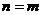 时,不等式成立,即
时,不等式成立,即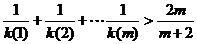
当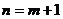 时,左边=
时,左边=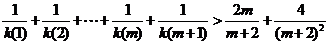
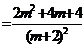
由
所以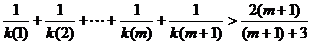
即当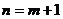 时,不等式也成立综上得
时,不等式也成立综上得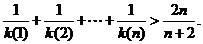
第三章 数系的扩充与复数的引入
第一讲 复数的相关概念和几何意义
[知识梳理]
[知识盘点]
1. 当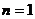 时,左边=1,右边=
时,左边=1,右边=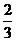 ,左边>右边,所以
,左边>右边,所以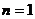 ,不等式成立
,不等式成立
22.解:(1)由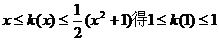 ,所以
,所以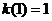
(2)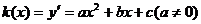 ,由
,由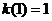 ,
,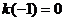 得
得
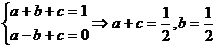
又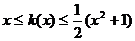 恒成立,则由
恒成立,则由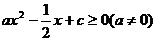 恒成立得
恒成立得
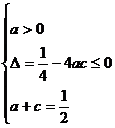
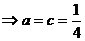 ,
,
同理由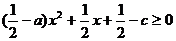 恒成立也可得:
恒成立也可得: 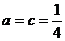
综上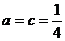 ,
, ,所以
,所以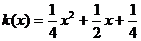
(3)证法一:(分析法)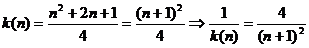
要证原不等式式,即证
因为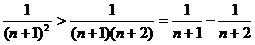
所以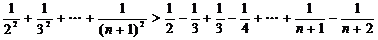
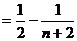 =
=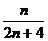
所以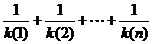
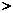
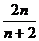
证法二(数学归纳法)由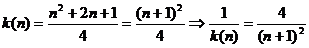
20.(1)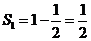 ,
,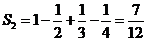
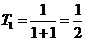 ,
,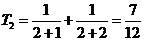
(2)猜想: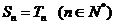 即:
即:
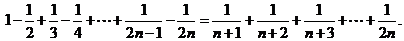 (n∈N*)
(n∈N*)
下面用数学归纳法证明:
① n=1时,已证S1=T1
② 假设n=k时,Sk=Tk(k≥1,k∈N*),即:
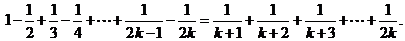
则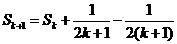
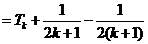
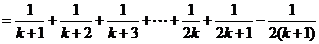
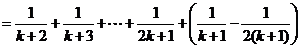
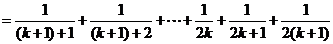
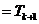
由①,②可知,对任意n∈N*,Sn=Tn都成立.

(2)归纳概括的结论为:
若数列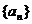 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则

19.解:当n=1时,由(n-1)an+1=(n+1)(an-1),得a1=1.
当n=2时,a2=6代入得a3=15.同理a4=28,再代入bn=an+n,有b1=2,b2=8,b3=18,b4=32,………,由此猜想bn=2n2. 要证bn=2n2,只需证an=2n2-n.
①当n=1时,a1=2×12-1=1成立.
②假设当n=k时,ak=2k2-k成立.
那么当n=k+1时,由(k-1)ak+1=(k+1)(ak-1),得a k+1=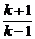 (ak-1)
(ak-1)
=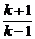 (2k2-k-1)=
(2k2-k-1)=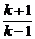 (2k+1)(k-1)=(k+1)(2k+1)=2(k+1)2-(k+1).
(2k+1)(k-1)=(k+1)(2k+1)=2(k+1)2-(k+1).
∴当n=k+1时,an=2n2-n正确,从而bn=2n2.
18.证明:要证明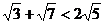 成立, 只需证
成立, 只需证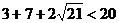 成立,
成立,
只需证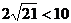 成立,只需证
成立,只需证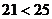 成立,上式显然成立,所以原命题成立.
成立,上式显然成立,所以原命题成立.
17.解:作差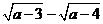
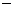 (
( )=
)=
∵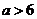 ,
,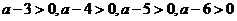 又∵
又∵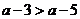 ∴
∴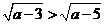
同样地有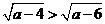 则
则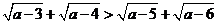
即知上式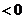 ∴
∴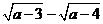 <
<
法二:令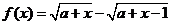 (
(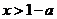 )
)
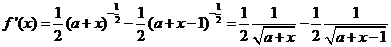 <0即知
<0即知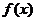 在定义域内为减函数,故
在定义域内为减函数,故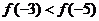 ,∴
,∴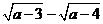 <
<
16.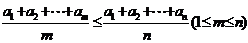 和
和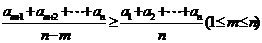
15.a+(a*b)=(a+b)*(a+c)(答案不惟一)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com