
1.A 2.C 3.A 4.C 5.A 6.B
12. [解]原方程化简为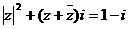 ,
,
设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi=1-i,
∴x2+y2=1且2x=-1,解得x=-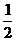 且y=±
且y=±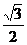 ,
,
∴原方程的解是z=-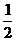 ±
±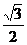 i.
i.
[仿真训练]
11. 解:由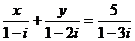 知,
知,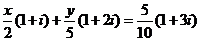 ,即
,即
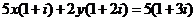 ,即
,即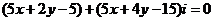 ,故
,故
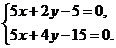 解得
解得
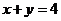 .
.
10.解法一:z,z2,z3,…,z7是一个等比数列.∴由等比数列求和公式可得: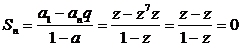 ,∴1+z+z2+z3+…+z6=0
,∴1+z+z2+z3+…+z6=0
解法二:S=1+z+z2+…+z6 ①
zS=z+z2+z3+…+z6+z7 ②
∴①-②得(1-z)S=1-z7=0
∴S=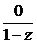 =0
=0
9.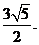
1.B 2.C 3.C 4.C 5.D 6.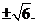 7.
7. 8.-1,2
8.-1,2
6. 证明:原方程化简为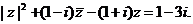 设
设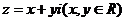 ,代入上述方程得:
,代入上述方程得: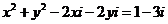 根据复数相等的充要条件,得
根据复数相等的充要条件,得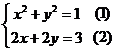 ,将(2)代入(1),整理得:
,将(2)代入(1),整理得: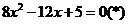 ,
,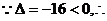 方程(
方程( )无实解,
)无实解,
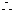 原方程在复数范围内无解。
原方程在复数范围内无解。
[能力提升]
5.解:由题意得 z1=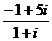 =2+3i,
=2+3i,
于是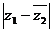 =
=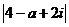 =
=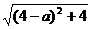 ,
,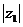 =
=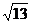 .
.
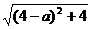 <
<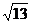 ,
,
得a2-8a+7<0,1<a<7.
4.解: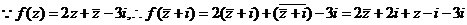
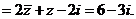
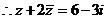 。
。
设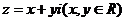 ,则
,则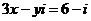
从而有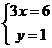 ,即
,即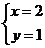 ,
,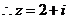 .
.
所以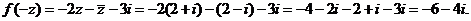
3. 解:∵|z1|>|z2|,∴x4+x2+1>(x2+a)2
∴(1-2a)x2+(1-a2)>0对x∈R恒成立
当1-2a=0,即a=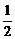 时,不等式成立;
时,不等式成立;
当1-2a≠0时,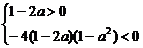
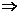 -1<a<
-1<a<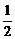

综上,a∈(-1,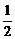 ]
]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com