例1 由数字1、2、3、4、5、6、7组成无重复数字的七位数

(1)求三个偶数必相邻的七位数的个数；

(2)求三个偶数互不相邻的七位数的个数

解 (1)：因为三个偶数2、4、6必须相邻，所以要得到一个符合条件的七位数可以分为如下三步：

第一步将1、3、5、7四个数字排好有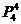种不同的排法；

第二步将2、4、6三个数字“捆绑”在一起有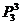 种不同的“捆绑”方法;

第三步将第二步“捆绑”的这个整体“插入”到第一步所排的四个不同数字的五个“间隙”(包括两端的两个位置)中的其中一个位置上,有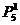种不同的“插入”方法

根据乘法原理共有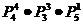＝720种不同的排法所以共有720个符合条件的七位数

解(2)：因为三个偶数2、4、6 互不相邻，所以要得到符合条件的七位数可以分为如下两步：

第一步将1、3、5、7四个数字排好，有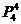 种不同的排法；

第二步将2、4、6分别“插入”到第一步排的四个数字的五个“间隙”(包括两端的两个位置)中的三个位置上，有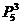 种“插入”方法

根据乘法原理共有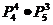＝1440种不同的排法所以共有1440个符合条件的七位数

例2　 将A、B、C、D、E、F分成三组，共有多少种不同的分法？

解：要将A、B、C、D、E、F分成三组，可以分为三类办法：

(1－1－4)分法、(1－2－3)分法、(2－2－2)分法

下面分别计算每一类的方法数：

第一类(1－1－4)分法，这是一类整体不等分局部等分的问题，可以采用两种解法

解法一：从六个元素中取出四个不同的元素构成一个组，余下的两个元素各作为一个组，有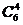种不同的分法

解法二：从六个元素中先取出一个元素作为一个组有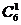 种选法，再从余下的五个元素中取出一个元素作为一个组有 种选法，最后余下的四个元素自然作为一个组，由于第一步和第二步各选取出一个元素分别作为一个组有先后之分，产生了重复计算，应除以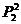

所以共有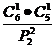 ＝15种不同的分组方法

　　 第二类(1－2－3)分法，这是一类整体和局部均不等分的问题，首先从六个不同的元素中选取出一个元素作为一个组有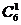 种不同的选法，再从余下的五个不同元素中选取出两个不同的元素作为一个组有 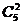种不同的选法，余下的最后三个元素自然作为一个组，根据乘法原理共有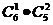＝60种不同的分组方法

　　 第三类(2－2－2)分法，这是一类整体“等分”的问题，首先从六个不同元素中选取出两个不同元素作为一个组有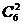 种不同的取法，再从余下的四个元素中取出两个不同的元素作为一个组有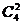种不同的取法，最后余下的两个元素自然作为一个组由于三组等分存在先后选取的不同的顺序，所以应除以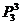 ，因此共有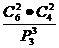 ＝15种不同的分组方法

　　 根据加法原理，将A、B、C、D、E、F六个元素分成三组共有：15+60+15＝90种不同的方法

例3 一排九个坐位有六个人坐，若每个空位两边都坐有人，共有多少种不同的坐法？

解：九个坐位六个人坐，空了三个坐位，每个空位两边都有人，等价于三个空位互不相邻，可以看做将六个人先依次坐好有种不同的坐法，再将三个空坐位“插入”到坐好的六个人之间的五个“间隙”(不包括两端)之中的三个不同的位置上有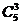种不同的“插入”方法

根据乘法原理共有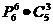 ＝7200种不同的坐法

解排列组合问题，首先要弄清一件事是“分类”还是“分步”完成，对于元素之间的关系，还要考虑“是有序”的还是“无序的”，也就是会正确使用分类计数原理和分步计数原理、排列定义和组合定义，其次，对一些复杂的带有附加条件的问题，需掌握以下几种常用的解题方法：

特殊优先法对于存在特殊元素或者特殊位置的排列组合问题，我们可以从这些特殊的东西入手，先解决特殊元素或特殊位置，再去解决其它元素或位置，这种解法叫做特殊优先法.例如：用0、1、2、3、4这5个数字，组成没有重复数字的三位数，其中偶数共有________个.(答案：30个)

科学分类法对于较复杂的排列组合问题，由于情况繁多，因此要对各种不同情况，进行科学分类，以便有条不紊地进行解答，避免重复或遗漏现象发生例如：从6台原装计算机和5台组装计算机中任取5台，其中至少有原装与组装计算机各两台，则不同的选取法有_______种.(答案：350)

插空法解决一些不相邻问题时，可以先排一些元素然后插入其余元素，使问题得以解决例如：7人站成一行，如果甲乙两人不相邻，则不同排法种数是______.(答案:3600)

捆绑法相邻元素的排列，可以采用“整体到局部”的排法，即将相邻的元素当成“一个”元素进行排列，然后再局部排列例如：6名同学坐成一排，其中甲、乙必须坐在一起的不同坐法是________种.(答案：240)

排除法从总体中排除不符合条件的方法数，这是一种间接解题的方法.

b、排列组合应用题往往和代数、三角、立体几何、平面解析几何的某些知识联系，从而增加了问题的综合性，解答这类应用题时，要注意使用相关知识对答案进行取舍.例如：从集合{0，1，2，3，5，7，11}中任取3个元素分别作为直线方程Ax+By+C=0中的A、B、C，所得的经过坐标原点的直线有_________条.(答案：30)

12．组合数的性质2：＝+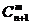　

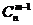
10．组合数公式：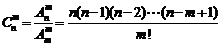

或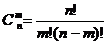

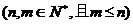
11 组合数的性质1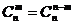：．规定：；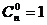

9．组合数的概念：从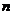个不同元素中取出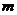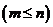个元素的所有组合的个数，叫做从 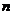个不同元素中取出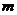个元素的组合数．用符号表示．

7．排列数的另一个计算公式：=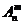

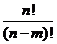
8组合的概念：一般地，从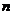个不同元素中取出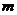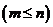个元素并成一组，叫做从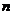个不同元素中取出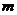个元素的一个组合

5．排列数公式：()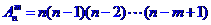

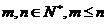6阶乘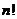：表示正整数1到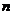的连乘积，叫做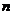的阶乘规定．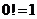

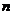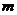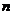4．排列数的定义：从个不同元素中，任取()个元素的所有排列的个数叫做从个元素中取出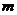元素的排列数，用符号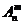表示

3．排列的概念：从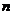个不同元素中，任取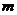()个元素(这里的被取元素各不相同)按照一定的顺序排成一列，叫做从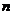个不同元素中取出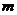个元素的一个排列

　　 1分类计数原理：做一件事情，完成它可以有n类办法，在第一类办法中有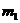种不同的方法，在第二类办法中有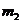种不同的方法，……，在第n类办法中有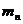种不同的方法那么完成这件事共有 种不同的方法

2.分步计数原理：做一件事情，完成它需要分成n个步骤，做第一步有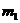种不同的方法，做第二步有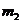种不同的方法，……，做第n步有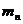种不同的方法，那么完成这件事有 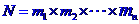种不同的方法