1. 线段CD是由线段AB平移得到的.点A(–1，4)的对应点为C(4，7)，则点B(– 4，– 1)的对应点D的坐标为(　　 )

A.(2，9)　　　 B.(5，3)　　 C.(1，2)　　　 D.(– 9，– 4)

5、考查用坐标表示平移

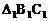例5 　(2008年湘潭)如图5，方格纸中的每个小方格都是边长为1个单位长度的正方形，我们把顶点在格点上的三角形称为“格点三角形”，图中的△ABC就是格点三角形.在建立平面直角坐标系以后，点B的坐标为(―1，―1).把△ABC向左平移3个格后得到，画出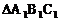，并分别写出点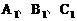的坐标

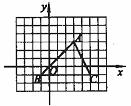
图5

解题思路：认真观察图5，可知A点的坐标为(3，3)，C点的坐标为(5，－1).图形向左平移3个单位，则原图形中各点纵坐标不变，横坐标减3，故可知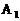(0，3)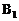，(―4，―1)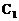，(2，－1).在平面直角坐标系中分别描出点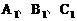，再顺次连接这三个点，即可得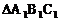(如图6).

点拨：若点P(x，y)向左(或向右)平移a(a>0)个单位，则对应点的横坐标是x减去(或加上)a，纵坐标不变；若向上(或向下)平移b(b>0)个单位，则对应点的横坐标不变，纵坐标是y加上(或减去)b.

过关测试

4、考查利用坐标确定点的位置

例4 (2009襄樊市) 将图4所示的围棋棋盘放在某个平面直角坐标系内，白棋②的坐标为(－7，－4)，白棋④的坐标为(―6，―8)，那么黑棋的坐标应该是_________.

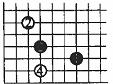
图4

解题思路：本题用围棋棋盘中正方形网格的相对位置来考查平面直角坐标系及点的坐标等相关知识.黑棋可看成是白棋④先向右平移3个单位，再向上平移1个单位，故可知其坐标为(―3，―7).应填(―3，―7).

点拨：用坐标确定平面内点的位置，需要先建立适当的平面直角坐标系.

3、考查平面直角坐标系中图形面积的计算

例3 (2009年常德市) 如图2，平面直角坐标系中，△ABC的顶点都在格点上(每个小方格的边长都为1cm).其中A点的坐标为(2，－1)，则△ABC的面积为______.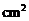

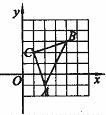
图2

解题思路：经观察可知点B的坐标为(4，3)，点C的坐标为(1，2).由于△ABC没有边与x轴或y轴平行，故需要用割补法将其补成图3中的矩形MNPB，即过点A、B分别作x轴的平行线，过点B、C分别作y轴的平行线，交点为P、N、M、B.可求得P(4，－1)，N(1，－1)，M(1，3)，则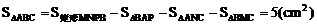.应填5.

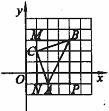
图3

点拨：计算平面直角坐标系内图形的面积时，常常把图形割补成边在坐标轴上或边与坐标轴平行的图形来计算面积.

2、考查坐标的计算

例2(2009年南充 ) 如图1，在平面直角坐标系中，平行四边形OABC的顶点O、A、C的坐标分别是(0，0)、(5，0)、(2，3)，则顶点B的坐标是(　　 ).

A、(3，7)　　　 B、(5，3)　　　 C、(7，3)　　　 D、(8，2)

图1

解题思路：根据点的坐标的确定方法，过点C分别作x轴和y轴的垂线，垂足分别为G、F.过点B分别作x轴和y轴的垂线，垂足分别为E、F.因为四边形OABC是平行四边形，CB//OA，且CB=OA，则四边形OGCF和四边形OEBF均为矩形，所以BE=CG=3，GE=CB=OA，BF=CB+CF=GE+OG=5+2=7，所以点B的坐标为(7，3)，故选C.

点拨：点的坐标是一对有序实数，过某一点作x轴的垂线，垂足所对应的数字即为它的横坐标，作y轴的垂线，垂足所对应的数字即为它的纵坐标.故要求点的坐标，就要求出这两个垂足所对应的数字.

1、考查平面内点的特征

例1 (2009年牡丹江市) 若点P(a，b)在第二象限，则点Q(―a，―b―1)在(　　 )

A、第一象限　　　　　 B、第二象限　　 C、第三象限　　 D、第四象限

解题思路：这是一道数形结合题，要根据各象限内点的坐标的符号特征来解.因为点P(a，b)在第二象限，所以a<0，b>0，于是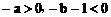，即点Q(―a，―b―1)在第四象限，故选D.

点拨：数形结合思想使几何图形和代数知识有机地结合在一起，使抽象的代数问题变得直观、形象，我们在解题时，要学会由形想到数，由数想到形.

2.关于y成轴对称的点的坐标，纵坐标相同，横坐标互为相反数.

3关于原点成中心对称的点的坐标，横坐标与横坐标互为相反数，纵坐标与纵坐标互为相反数.

例1、点M(5，－6)关于x轴的对称点的坐标是( )．

　(A)(－6，5)　　(B)(－5，－6)

　(C)(5，6)　　(D)(－5，6)

　例2、点N(a，-b)关于原点的对称点是坐标是( ).

　(A)(-a，b)　　(B)(-a，-b)

　(C)(a，b)　　(D)(-b，a)

　解题思路：例1把点M(5，-6)和选项中的四个点都描在同一坐标系内，可发现只有点(5，6)和M点关于x轴对称，因此选C．

　另法：点M(5，-6)在第四象限，和点M关于x轴对称的点应在第一象限，选项中只有点(5，6)在第一象限，因此选C．

　方法三：两个点关于x轴对称，它们的横坐标相同，纵坐标互为相反数，反之也对．在选项中的四个点，只有点(5，6)符合题意．因此选C．

　例2两个点关于原点对称，它们的横坐标互为相反数，纵坐标也互为相反数，反之也对．选项中只有点(-a，b)符合题意，因此选A．

　另法：或令a＝1，b＝1，则N点的坐标为(1，－1)在第四象限，和N关于原点对称的点应在第二象限，其坐标为(-1，1)只有(-a，b)合题意，因此选A．

最新考题

从近几年的中考看，直接考查本讲的题目约占4%左右，题型有选择、填空、解答等，本讲知识是今后复习函数及其图像等知识的基础，因此中考常常结合相关知识综合命题，平面直角坐标系相关知识与地理问题相结合，但实质仍为坐标问题，借助坐标系中点与坐标的对应关系来确定位置.平面直角坐标系中确定点的位置问题，是近年来中考命题的重点多以选择题、填空题形式出现.

例1当b=______时,点B(3,|b-1|)在第一.三象限角平分线上.

例2当b=______时,点B(3,b-1)在第二.四象限角平分线上.

解题思路：运用象限的角平分线上点的坐标特征，例1、|b-1|=3，b=4或-2；例2、b-1+3=0，则b=-2

练习

已知点A(3x-2y，y+1)在象限的角平分线上，且点A的横坐标为5，求x、y的值

答案：x=13/3,y=4或-7/3，y=-6

知识点6、点到x轴，y轴的距离

点P(x,y)到x轴，y轴的距离分别为|y|和|x|,到原点的距离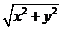

例M为X轴上方的点，到X轴距离为5，到Y 的距离为3，则M点的坐标为(　　　 ).

A(5，3)　 B(-5，3)或(5，3)

C(3，5)　 D(-3，5)或(3，5)

解题思路：结合坐标系，注意不同的情况，选D

练习

在平面直角坐标系中，点A到横轴的距离为8，到纵轴的距离为4，则点A的坐标为----；

答案：(4，8)或(-4，8)或(-4，-8)或(4，-8)

知识点7、平移问题：

重点：掌握平移的规律　 难点：平移规律的运用

1 点的平移：

在平面直角坐标系中，将点( x,y )向右(或左)平移 a 个单位长度，可以得到对应点( x+a, y ) ( 或(x-a，y) ) ；将点( x, y )向上(或下)平移 b 个单位长度，可以得到对应点 (x, y+b) ( 或(x, y-b) ) .

2 图形的平移：

在平面直角坐标系内，如果把一个图形各个点的横坐标都加(或减)一个正数 a ，相应的新图形就是把原图形向右(或向 左)平移a个单位长度；如果把它各个点的纵坐标都加(或减)一个正数 a ，相应的新图形就是把原图形向上(或向下)平移a 个单位长度.

例1已知正方形ABCD的三个顶点坐标为A(2，1)，B(5，1)，D(2,4),现将该正方形向下平移3个单位长度，再向左平移4个单位长度，得到正方形A'B'C'D'，则C’点的坐标为(　 )

　 A. (5，4)　　 B. (5，1)　　 C. (1，1)　　 D. (-1，-1)

例2. 适当建立直角坐标系，描出点(0，0)，(5，4)，(3，0)，(5，1)，(5，-1)，(3，0)，(4，-2)，(0，0)，并用线段顺次连接各点.

⑴. 看图案像什么？

⑵. 作如下变化：纵坐标不变，横坐标减2，并顺次连接各点，所得的图案与原来相比有什么变化？

解题思路：运用平移的规律：如果把一个图形各个点的横坐标都加(或减)一个正数 a ，相应的新图形就是把原图形向右(或向 左)平移a个单位长度；如果把它各个点的纵坐标都加(或减)一个正数 a ，相应的新图形就是把原图形向上(或向下)平移a 个单位长度.

例1、选C 例2、图略(1). 像“鱼”、(2)图案向左平移两个单位

知识点8、平面直角坐标系中对称点的特点

重点：掌握平面直角坐标系中对称点的特点

　难点：对称点的特点的运用

1.关于x成轴对称的点的坐标，横坐标相同，纵坐标互为相反数.

30、(10分)工业上以黄铁矿为原料生产硫酸，其中重要的一步是催化氧化：

2SO₂(g)+O₂ (g)2SO₃(g) △H＝－196.6 kJ·mol^－1

(1)生产中为提高反应速率和SO₂的转化率，下列措施可行的是　 　　　(填字母)。

A．向装置中充入N₂B．向装置中充入过量的O₂

C．使用更高效的催化剂　　　　　 D．升高温度

(2)在一密闭容器中充入4 mol SO₂和一定量O₂，当放出353.6 kJ热量时，SO₂的转化率最接近于　 　　　(填字母)。

　　 A．40%　　　　 B．50%　　　　 C．80%　　　　　 D．90%

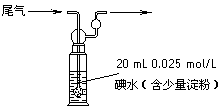(3)580℃时，在一密闭容器中充入一定量的SO₂和O₂，当反应达到平衡后测得SO₂、O₂和SO₃的浓度分别为6.0×10^－3 mol·L^－1、8.0×10^－3 mol·L^－1和4.4×10^－2 mol·L^－1。该温度下反应2SO₂(g)+O₂ (g)2SO₃(g)的平衡常数K＝　 　　　　　　　　　　。

(4)硫酸工业尾气中二氧化硫含量超过0.05%(体积分数)时需要加以处理后才能排放。现用右图所示装置测定尾气中SO₂的含量，当通入尾气11.2 L(标准状况下测定)时，碘水恰好褪色。通过计算说明，该尾气能否直接排放(写出计算过程)。

嘉兴市南湖高级中学2010学年(上)高三第一次月考

28、(8分)推断化合物的化学性质，常从两个角度分析：

Ⅰ、物质的属类(如氧化物、酸、碱或盐等)；

Ⅱ、组成元素的化合价(是否处于最高价、中间价态或最低价)。请回答：

(1)已知SO₂是一种酸性氧化物，试写出一个化学方程式表示该物质具有的化学性质　

　　　　　　　　　　　　　　　　　　　　　　 ；

(2)根据硝酸中氮元素的化合价，可以预测硝酸一定具有　 　　　　　；(填字母)

A、氧化性　　　　　 B、还原性

①你推断的理由是　 　　　　　　　　　　　。

②以浓硝酸为例，写出一个符合你预测的化学方程式　 　　　　　　　　　　　　　。

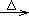甲　　　　 乙丙甲

(1)若甲是不溶于水的白色粉末状氧化物，既能溶于盐酸又能溶于氢氧化钠溶液，则甲物质是 　　　　　　　；丙物质是　 　　　　　　。(用化学式表示)

写出“乙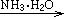丙”转化的化学方程式　 　　　　　　　　　　　　　　　　。

(2)若乙溶液中加入KSCN溶液，有血红色出现，则甲物质是_____　　 ___；丙物质是　 　　　　　　。(用化学式表示)

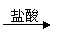写出“甲　　　　 乙”转化的离子方程式　 　　　　　　　　　　　　　　　　　。

写出甲与CO在高温下发生反应的化学方程式　 　　　　　　　　　　　　　　。