(一)创设情景，揭示课题．

我们在前两节课中，已经学习了函数的定义，会求函数的值域，那么函数有哪些表示的方法呢？这一节课我们研究这一问题．

2．教学用具：圆规、三角板、投影仪．

1．学法：学生通过观察、思考、比较和概括，从而更好地完成本节课的教学目标．

教学重点：函数的三种表示方法，分段函数的概念．

教学难点：根据不同的需要选择恰当的方法表示函数，什么才算“恰当”？分段函数的表示及其图象．

3．情态与价值

让学生感受到学习函数表示的必要性，渗透数形结合思想方法。

2．过程与方法：

学习函数的表示形式，其目的不仅是研究函数的性质和应用的需要，而且是为加深理解函数概念的形成过程．

1．知识与技能

(1)明确函数的三种表示方法；

(2)会根据不同实际情境选择合适的方法表示函数；

(3)通过具体实例，了解简单的分段函数及应用．

(六)设置问题，留下悬念

1、课本P₂₈ 习题1．2(A组) 第1-7题 (B组)第1题

2、举出生活中函数的例子(三个以上)，并用集合与对应的语言来描述函数，同时说出函数的定义域、值域和对应关系。

§1．2．2函数的表示法

(五)归纳小结

①从具体实例引入了函数的概念，用集合与对应的语言描述了函数的定义及其相关概念；②初步介绍了求函数定义域和判断同一函数的基本方法，同时引出了区间的概念。

(四)巩固深化，反馈矫正：

(1)课本P₂₂第2题

(2)判断下列函数f(x)与g(x)是否表示同一个函数，说明理由？

① f ( x ) = (x －1) ⁰；g ( x ) = 1

② f ( x ) = x； g ( x ) =

③ f ( x ) = x ²；f ( x ) = (x + 1) ²

④ f ( x ) = | x | ；g ( x ) =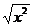

(3)求下列函数的定义域

①

②

③ f(x) = +

④ f(x) =

⑤