
1. 教材注重从现实生活的事例中引出指数函数概念,所举例子比较全面,有利于培养学生的思想素质和激发学生学习数学的兴趣和欲望. 教学中要充分发挥课本的这些材料的作用,并尽可能联系一些熟悉的事例,以丰富教学的情景创设.
8.
通过实例,了解幂函数的概念,结合五种具体函数 的图象,了解它们的变化情况 .
的图象,了解它们的变化情况 .
7. 知道指数函数y=ax与对数函数y=logax互为反函数(a>0, a≠1),初步了解反函数的概念和f- -1(x)的意义.
6. 通过具体函数,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,掌握f(x)=logax符号及意义,体会对数函数是一类重要的函数模型,能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的有关性质(单调性、值域、特殊点).
4. 通过应用实例的教学,体会指数函数是一种重要的函数模型.
3. 理解指数函数的概念和意义,掌握f(x)=ax的符号、意义,能借助计算器或计算机画出具体指数函数的图象,探索并理解指数函数的有关性质(单调性、值域、特别点).
2. 理解有理数指数幂的意义,通过具体实例了解实数指数幂的意义,掌握幂的运算.
教材把指数函数,对数函数,幂函数当作三种重要的函数模型来学习,强调通过实例和图象的直观,揭示这三种函数模型增长的差异及其关系,体会建立和研究一个函数模型的基本过程和方法,学会运用具体函数模型解决一些实际问题.
1. 了解指数函数模型的实际背景.
(六)设置问题,留下悬念.
1.书面作业:课本P46习题A组1.3.9.10题
2.设 >0时,
>0时,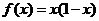
试问:当 <0时,
<0时, 的表达式是什么?
的表达式是什么?
解:当 <0时,-
<0时,- >0,所以
>0,所以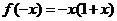 ,又因为
,又因为 是奇函数,所以
是奇函数,所以
 .
.
第二章 基本初等函数(Ⅰ)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com