
2.过程与方法
类比研究一般函数,指数函数、对数函数的过程与方法,后研幂函数的图象和性质.
1.知识技能
(1)理解幂函数的概念;
(2)通过具体实例了解幂函数的图象和性质,并能进行初步的应用.
3.由上述探究你能得出什么结论,此结论对于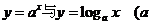 >0
>0 成立吗?
成立吗?
幂函数
2.取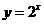 图象上的几个点,写出它们关于直线
图象上的几个点,写出它们关于直线 的对称点坐标,并判断它们
的对称点坐标,并判断它们
是否在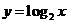 的图象上吗?为什么?
的图象上吗?为什么?
1.在同一平面直角坐标系中,画出 的图象,你能发现这两个函数有什么样的对称性吗?
的图象,你能发现这两个函数有什么样的对称性吗?
2.你怎样理解反函数?
课后思考:(供学有余力的学生练习)
我们知道 >0
>0 与对数函数
与对数函数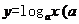 >0且
>0且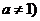 互为反函数,探索下列问题.
互为反函数,探索下列问题.
3.引出反函数的概念(只让学生理解,加宽学生视野)
当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数为反函数.
由反函数的概念可知,同底的指数函数和对数函数互为反函数.
如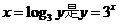 的反函数,但习惯上,通常以
的反函数,但习惯上,通常以 表示自变量,
表示自变量, 表示函数,对调
表示函数,对调 中的
中的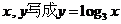 ,这样
,这样 是指数函数
是指数函数 的反函数.
的反函数.
以后,我们所说的反函数是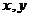 对调后的函数,如
对调后的函数,如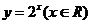 的反函数是
的反函数是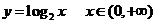 .
.
同理,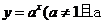 >1)的反函数是
>1)的反函数是 >0且
>0且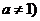 .
.
课堂练习:求下列函数的反函数
(1) (2)
(2)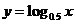
归纳小结: 1. 今天我们主要学习了什么?
2.讲授新知
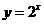
 |
… |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
 |
… |
 |
 |
 |
1 |
2 |
4 |
8 |
… |
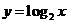
 |
… |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
… |
 |
… |
 |
 |
 |
1 |
2 |
4 |
8 |
… |
图象如下:

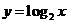
|
|
||||
探究:在指数函数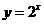 中,
中, 为自变量,
为自变量, 为因变量,如果把
为因变量,如果把 当成自变量,
当成自变量, 当成因变量,那么
当成因变量,那么 是
是 的函数吗?如果是,那么对应关系是什么?如果不是,请说明理由.
的函数吗?如果是,那么对应关系是什么?如果不是,请说明理由.
引导学生通过观察、类比、思考与交流,得出结论.
在指数函数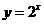 中,
中, 是自变量,
是自变量,  是
是 的函数(
的函数( ),而且其在R上是单调递增函数. 过
),而且其在R上是单调递增函数. 过 轴正半轴上任意一点作
轴正半轴上任意一点作 轴的平行线,与
轴的平行线,与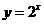 的图象有且只有一个交点.由指数式与对数式关系,
的图象有且只有一个交点.由指数式与对数式关系, ,即对于每一个
,即对于每一个 ,在关系式
,在关系式 的作用之下,都有唯一的确定的值
的作用之下,都有唯一的确定的值 和它对应,所以,可以把
和它对应,所以,可以把 作为自变量,
作为自变量, 作为
作为 的函数,我们说
的函数,我们说 .
.
从我们的列表中知道, 是同一个函数图象.
是同一个函数图象.
1.复习
(1)函数的概念
(2)用列表描点法在同一个直角坐标点中画出 的函数图象.`
的函数图象.`
学法:通过图象,理解对数函数与指数函数的关系.
教具:多媒体
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com