
2. 教学难点:将实际问题转变为数学模型.
1.教学重点:运用一次函数、二次函数模型解决一些实际问题.
3.情感、态度、价值观 体会运用函数思想处理现实生活中和社会中的一些简单问题的实用价值.
2.过程与方法 感受运用函数概念建立模型的过程和方法,体会一次函数、二次函数模型在数学和其他学科中的重要性.
1. 知识与技能 能够找出简单实际问题中的函数关系式,初步体会应用一次函数、二次函数模型解决实际问题.
(五)布置作业
教材P119练习第2题
收集一些社会生活中普遍使用的递增的一次函数、指数函数、对数函数的实例,对它们的增长速度进行比较,了解函数模型的广泛应用,并思考。有时同一个实际问题可以建立多个函数模型,在具体应用函数模型时,应该怎样选用合理的函数模型.
§3.2.2 函数模型的应用实例(Ⅰ)
(四)归纳总结,提升认识.
教师通过计算机作图进行总结,使学生认识直线上升、指数爆炸、对数增长等不同函数模型的含义及其差异,认识数学与现实生活、与其他学科的密切联系,从而体会数学的实用价值和内在变化规律.
(三)实例运用,巩固提高.
1. 教师引导学生分析影响方案选择的因素,使学生认识到要做出正确选择除了考虑每天的收益,还要考虑一段时间内的总收益. 学生通过自主活动,分析整理数据,并根据其中的信息做出推理判断,获得累计收益并给出本例的完整解答,然后全班进行交流.
2. 教师引导学生分析例2中三种函数的不同增长情况对于奖励模型的影响,使学生明确问题的实质就是比较三个函数的增长情况,进一步体会三种基本函数模型在实际中广泛应用,体会它们的增长差异.
3.教师引导学生分析得出:要对每一个奖励模型的奖金总额是否超出5万元,以及奖励比例是否超过25%进行分析,才能做出正确选择,学会对数据的特点与作用进行分析、判断。
4.教师引导学生利用解析式,结合图象,对例2的三个模型的增长情况进行分析比较,写出完整的解答过程. 进一步认识三个函数模型的增长差异,并掌握解答的规范要求.
5.教师引导学生通过以上具体函数进行比较分析,探究幂函数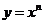 (
( >0)、指数函数
>0)、指数函数 (
( >1)、对数函数
>1)、对数函数 (
( >1)在区间(0,+∞)上的增长差异,并从函数的性质上进行研究、论证,同学之间进行交流总结,形成结论性报告. 教师对学生的结论进行评析,借助信息技术手段进行验证演示.
>1)在区间(0,+∞)上的增长差异,并从函数的性质上进行研究、论证,同学之间进行交流总结,形成结论性报告. 教师对学生的结论进行评析,借助信息技术手段进行验证演示.
6. 课堂练习
教材P116练习1、2,并由学生演示,进行讲评。
(二)互动交流,探求新知.
1. 观察数据,体会模型.
教师引导学生观察例1表格中三种方案的数量变化情况,体会三种函数的增长差异,说出自己的发现,并进行交流.
2. 作出图象,描述特点.
教师引导学生借助计算器作出三个方案的函数图象,分析三种方案的不同变化趋势,并进行描述,为方案选择提供依据.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com