
1. 当0≤x≤1时,函数y=ax+a-1的值有正值也有负值,则实数a的取值范围是 (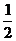 ,1)
,1)
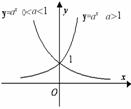
5.幂函数
(1)幂函数的定义: 形如y=x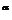 (
( 为常量)。
为常量)。
(2)幂函数的性质:
所有幂函数在 (0,+ )上都有意义,并且图像都过点
(1,1) 。
)上都有意义,并且图像都过点
(1,1) 。
(3)幂函数 ,当
,当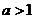 时,若
时,若 其图像在直线
其图像在直线 的下方,若
的下方,若 ,其图像在直线
,其图像在直线 的上方;当
的上方;当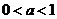 时,若
时,若 其图像在直线
其图像在直线 的上方,当
的上方,当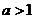 时,若
时,若 其图像在直线
其图像在直线 的下方。幂函数图像在第一象限的特点: 正抛负双,大上小右
的下方。幂函数图像在第一象限的特点: 正抛负双,大上小右
课前预习
4.对数函数:如果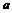 (
( )的
)的 次幂等于
次幂等于 ,就是
,就是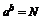 ,数
,数 就叫做以
就叫做以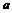 为底的
为底的 的对数,记作
的对数,记作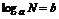 (
( ,负数和零没有对数);其中
,负数和零没有对数);其中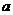 叫底数,
叫底数, 叫真数.
叫真数.
⑴对数运算:


⑵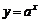 (
(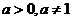 )与
)与 互为反函数.
互为反函数.
当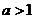 时,
时, 的
的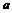 值越大,越靠近
值越大,越靠近 轴;当
轴;当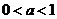 时,则相反.
时,则相反.
3. 指数函数:
指数函数: (
(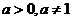 ),定义域R,值域为(
),定义域R,值域为( ).⑴①当
).⑴①当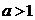 ,指数函数:
,指数函数: 在定义域上为增函数;②当
在定义域上为增函数;②当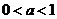 ,指数函数:
,指数函数: 在定义域上为减函数.⑵当
在定义域上为减函数.⑵当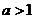 时,
时,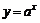 的
的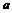 值越大,越靠近
值越大,越靠近 轴;当
轴;当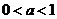 时,则相反.
时,则相反.
2.一元二次函数:
一般式: ;对称轴方程是
;对称轴方程是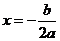 ;顶点为
;顶点为 ;
;
两点式: ;对称轴方程是 ;与
;对称轴方程是 ;与 轴的交点为
;
轴的交点为
;
顶点式: ;对称轴方程是
;顶点为
;
;对称轴方程是
;顶点为
;
⑴一元二次函数的单调性:
当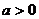 时: 为增函数; 为减函数;
时: 为增函数; 为减函数;
当 时: 为增函数; 为减函数;
时: 为增函数; 为减函数;
⑵二次函数求最值问题:首先要采用配方法,化为 的形式,
的形式,
⑶二次方程实数根的分布问题:
注:常见的初等函数一次函数,二次函数,反比例函数,指数函数,对数函数。
特别指出,分段函数也是重要的函数模型。
1.一元一次函数: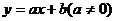 ,当
,当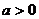 时,是增函数;当
时,是增函数;当 时,是减函数;
时,是减函数;
6.(08北京模拟)若函数 的定义域、值域都是闭区间[2,2b],则b的
的定义域、值域都是闭区间[2,2b],则b的
为 2 。
7 (08北京模拟)对于任意实数 ,
, ,定义
,定义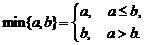 设函数
设函数
 ,则函数
,则函数 的最大值是___1_______
.
的最大值是___1_______
.
5、(07浙江文11)函数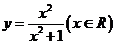 的值域是__
的值域是__ _.
_.
4、(07上海理1)函数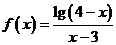 的定义域为{x|x<4且x
的定义域为{x|x<4且x 3}
3}
3、(07北京文14)已知函数 ,
, 分别由下表给出
分别由下表给出
 |
1 |
2 |
3 |
 |
2 |
1 |
1 |
 |
1 |
2 |
3 |
 |
3 |
2 |
1 |
则 的值为 1 ;当
的值为 1 ;当 时,
时, 1 .
1 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com