
5.如图所示的是某池塘中的浮萍蔓延的面积y(m 2)与时间t(月)的关系:y=at,有以下叙述:①这个指数函数的底数为2;②第5
个月时,浮萍面积就会超过30 m2;③浮萍从4 m2蔓延到12 m2需要经过1.5个月;④浮萍每月增加的面积都相等;⑤若浮萍蔓延到2 m2、3 m2、6 m2所经过的时间分别为t1、t2、t3,则t1+t2=t3.其中正确的是 ( )
 ?A.①②
?B.①②③④
?A.①②
?B.①②③④
?C.②③④⑤ ?D.①②⑤
答案?D?

例1计算:(1)
(2)2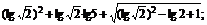
(3)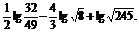
解 (1)方法一 利用对数定义求值
设
则
∴x=-1.
方法二 利用对数的运算性质求解

(2)原式=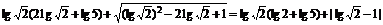
=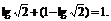
(3)原式=
=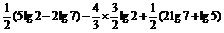
=
=
例2比较下列各组数的大小.
(1)log3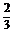 与log5
与log5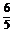 ;
;
(2)log1.10.7与log1.20.7;
(3)已知 比较2b,2a,2c的大小关系.
比较2b,2a,2c的大小关系.
解 (1)∵log3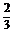 <log31=0,
<log31=0,
而log5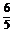 >log51=0,∴log3
>log51=0,∴log3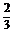 <log5
<log5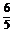 .
.
(2)方法一 ∵0<0.7<1,1.1<1.2,
∴0>log0.71.1>log0.71.2,
∴
即由换底公式可得log1.10.7<log1.20.7.
 方法二 作出y=log1.1x与y=log1.2x的图象.
方法二 作出y=log1.1x与y=log1.2x的图象.
如图所示两图象与x=0.7相交可知log1.10.7<log1.20.7.
(3)∵y=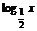 为减函数,且
为减函数,且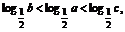
∴b>a>c,而y=2x是增函数,∴2b>2a>2c.
例3(12分)已知函数f(x)=logax (a>0,a≠1),如果对于任意x∈[3,+∞)都有|f(x)|≥1成立,试求a的取值范围.
解 当a>1时,对于任意x∈[3,+∞),都有f(x)>0.
所以,|f(x)|=f(x),而f(x)=logax在[3,+∞)上为增函数,
∴对于任意x∈[3,+∞),有f(x)≥loga3. 4分
因此,要使|f(x)|≥1对于任意x∈[3,+∞)都成立.
只要loga3≥1=logaa即可,∴1<a≤3. 6分
当0<a<1时,对于x∈[3,+∞),有f(x)<0,
∴|f(x)|=-f(x). 8分
∵f(x)=logax在[3,+∞)上为减函数,
∴-f(x)在[3,+∞)上为增函数.
∴对于任意x∈[3,+∞)都有|f(x)|=-f(x)≥-loga3. 10分
因此,要使|f(x)|≥1对于任意x∈[3,+∞)都成立,
只要-loga3≥1成立即可,
∴loga3≤-1=loga ,即
,即 ≤3,∴
≤3,∴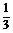 ≤a<1.
≤a<1.
综上,使|f(x)|≥1对任意x∈[3,+∞)都成立的a的取值范围是:(1,3]∪[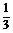 ,1).
12分
,1).
12分
例4 已知过原点O的一条直线与函数y=log8x的图象交于A、B两点,分别过A、B作y轴的平行线与函数y=log2x的图象交于C、D两点.
(1)证明:点C、D和原点O在同一直线上;
(2)当BC平行于x轴时,求点A的坐标.
(1)证明 设点A、B的横坐标分别为x1、x2,
由题设知x1>1,x2>1,
则点A、B的纵坐标分别为log8x1、log8x2.
因为A、B在过点O的直线上,
所以
点C、D的坐标分别为(x1,log2x1)、(x2,log2x2),
由于log2x1=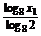 =3log8x1,log2x2=3log8x2,
=3log8x1,log2x2=3log8x2,
OC的斜率为k1=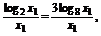
OD的斜率为k2=
由此可知k1=k2,即O、C、D在同一直线上.
(2)解 由于BC平行于x轴,知log2x1=log8x2,
即得log2x1=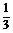 log2x2,x2=
log2x2,x2= ,
,
代入x2log8x1=x1log8x2,得
由于x1>1,知log8x1≠0,故 =3x1,
=3x1,
又因x1>1,解得x1=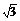 ,
,
于是点A的坐标为(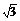 ,log8
,log8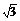 ).
).

4.若f(x)=logax在[2,+∞)上恒有f(x)>1,则实数a的取值范围是 ( )
?A.(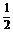 ,1) ?
B.(0,
,1) ?
B.(0,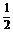 )∪(1,2)
)∪(1,2)
?C.(1,2) ?
D.(0,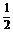 )∪(2,+∞)
)∪(2,+∞)
答案?C?
3.已知log7[log3(log2x)]=0,那么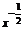 等于
( )
等于
( )
?A.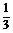 ?B.
?B. ?
C.
?
C. ?
D.
?
D.
答案?C?
2.已知3a=5b=A,且 =2,则A的值是
( )
=2,则A的值是
( )
?A.15
B. ?
C.±
?
C.± ?
D.225
?
D.225
答案?B?
1.(2008·全国Ⅱ理,4)若x∈(e-1,1),a=lnx,b=2lnx,c=ln3x,则 ( )
?A.a<b<c ?B.c<a<b ?C.b<a<c ?D.b<c<a
答案?C?
12.已知f(x)=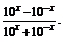
(1)判断函数奇偶性;
(2)证明:f(x)是定义域内的增函数;
(3)求f(x)的值域.
(1)解 ∵f(x)的定义域为R,
且f(-x)=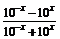 =-f(x),
=-f(x),
∴f(x)是奇函数.
(2)证明 方法一 f(x)=
令x2>x1,则f(x2)-f(x1)
=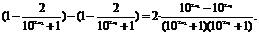
当x2>x1时, >0.
>0.
又∵ +1>0,
+1>0, >0,
>0,
故当x2>x1时,f(x2)-f(x1)>0,
即f(x2)>f(x1).所以f(x)是增函数.
方法二 考虑复合函数的增减性.
由f(x)=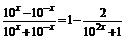 .
.
∵y1=10x为增函数,
∴y2=102x+1为增函数,y3= 为减函数,
为减函数,
y4=- 为增函数,
为增函数,
f(x)=1- 为增函数.
为增函数.
∴f(x)= 在定义域内是增函数.
在定义域内是增函数.
(3)解 方法一 令y=f(x),由y=
解得
∵102x>0,∴-1<y<1.
即f(x)的值域为(-1,1).
方法二 ∵f(x)=1- ,∵102x>0,∴102x+1>1.
,∵102x>0,∴102x+1>1.
∴0< <2,∴-1<1-
<2,∴-1<1- <1,
<1,
即值域为(-1,1).
§2.5 对数与对数函数

 基础自测
基础自测
11.已知函数f(x)=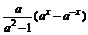 (a>0,且a≠1).
(a>0,且a≠1).
(1)判断f(x)的单调性;
(2)验证性质f(-x)=-f(x),当x∈(-1,1)时,并应用该性质求满足f(1-m)+f(1-m2)<0的实数m的范围.
解 (1)设x1<x2,x1-x2<0,1+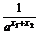 >0.
>0.
若a>1,则 >0,
>0,
所以f(x1)-f(x2)= <0,
<0,
即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数;
同理,若0<a<1,则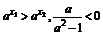 ,
,
f(x1)-f(x2)=
即f(x1)<f(x2),f(x)在(-∞,+∞)上为增函数.
综上,f(x)在R上为增函数.
(2)f(x)=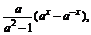
则f(-x)= 
显然f(-x)=-f(x).
f(1-m)+f(1-m2)<0,
即f(1-m)<-f(1-m2)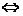 f(1-m)<f(m2-1),
f(1-m)<f(m2-1),
函数为增函数,且x∈(-1,1),
故解-1<1-m<m2-1<1,可得1<m< .
.
10.已知函数f(x)=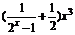
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)证明:f(x)>0.
(1)解 由2x-1≠0,得x≠0,
∴定义域为(-∞,0)∪(0,+∞).
(2)解 由(1)得,f(x)的定义域关于原点对称,
f(x)= 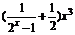 =
=
则f(-x)=
∴f(x)= 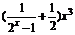 是偶函数.
是偶函数.
(3)证明 当x>0时,2x>1,x3>0.
∴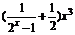 >0.
>0.
∵f(x)为偶函数,∴当x<0时,f(x)=f(-x)>0.
综上可得f(x)>0.
9.要使函数y=1+2x+4xa在x∈(-∞,1]上y>0恒成立,求a的取值范围.
解 由题意得1+2x+4xa>0在x∈(-∞,1]上恒成立,即a>- 在x∈(-∞,1]上恒成立.
在x∈(-∞,1]上恒成立.
又∵-
∵x∈(-∞,1],∴(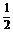 )x∈[
)x∈[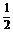 ,+∞).
,+∞).
令t=(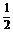 )x,则f(t)=-(t+
)x,则f(t)=-(t+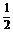 )2+
)2+ ,
,
t∈[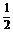 ,+∞),
,+∞),
则f(t)在[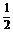 ,+∞)上为减函数,
,+∞)上为减函数,
f(t)≤f(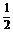 )=-(
)=-(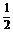 +
+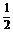 )2 +
)2 + ,
,
即f(t)∈(-∞,-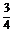 ].
].
∵a>f(t),∴a∈(-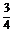 ,+∞).
,+∞).
8.函数y=ax(a>0,且a≠1)在[1,2]上的最大值比最小值大 ,则a的值是 .
,则a的值是 .
答案 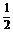 或
或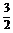
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com