
4.若幂函数f(x)的图象经过点(3,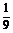 ),则其定义域为 ( )
),则其定义域为 ( )
A.{x|x∈R, x>0} B. {x|x∈R, x<0}
C. {x|x∈R,且x≠0} D.R
答案 C
3.下列说法正确的是 ( )
A.幂函数一定是奇函数或偶函数
B.任意两个幂函数图象都有两个以上交点
C.如果两个幂函数的图象有三个公共点,那么这两个幂函数相同
? D.图象不经过(-1,1)的幂函数一定不是偶函数
答案 D
2.(2008·山东文,4)给出命题:若函数y=f(x)是幂函数,则函数y=f(x)的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是 ( )
A.3 B.2 C.1 D.0
答案 C
1.下列函数中:①y= ②y=3x-2;③y=x4+x2;④y=
②y=3x-2;③y=x4+x2;④y=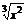 是幂函数的个数为
( )
是幂函数的个数为
( )
A.1 B.2 C.3 D.4
答案 B
12.已知函数f(x)=loga (a>0,且a≠1,b>0).
(a>0,且a≠1,b>0).
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)讨论f(x)的单调性.
解 (1)由 >0
>0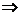 (x+b)(x-b)>0.
(x+b)(x-b)>0.
解得f(x)的定义域为(-∞,-b)∪(b,+∞).
(2)∵f(-x)=loga
∴f(x)为奇函数.
(3)令u(x)= ,则u(x)=1+
,则u(x)=1+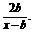
它在(-∞,-b)和(b,+∞)上是减函数.
∴当0<a<1时,f(x)分别在(-∞,-b)和(b,+∞)上是增函数;
当a>1时,f(x)分别在(-∞,-b)和(b,+∞)上是减函数.
§2.6幂函数

 基础自测
基础自测
11.已知定义域为R的函数f(x)为奇函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(log 24).
24).
解 (1)令x∈[-1,0),则-x∈(0,1],∴f(-x)=2-x-1.
又∵f(x)是奇函数,∴f(-x)=-f(x),∴-f(x)=f(-x)=2-x-1,
∴f(x)=-(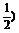 x+1.
x+1.
(2)∵f(x+2)=-f(x),∴f(x+4)=-f(x+2)=f(x),∴f(x)是以4为周期的周期函数,
∵log 24=-log224∈(-5,-4),∴log
24=-log224∈(-5,-4),∴log 24+4∈(-1,0),
24+4∈(-1,0),
∴f(log 24)=f(log
24)=f(log 24+4)=-(
24+4)=-(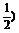
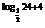 +1=-24×
+1=-24× +1=-
+1=-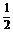 .
.
10.已知函数y=log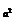 (x2-2ax-3)在(-∞,-2)上是增函数,求a的取值范围.
(x2-2ax-3)在(-∞,-2)上是增函数,求a的取值范围.
解 因为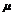 (x)=x2-2ax-3在(-∞,a]上是减函数,
(x)=x2-2ax-3在(-∞,a]上是减函数,
在[a,+∞)上是增函数,
要使y= log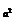 (x2-2ax-3)在(-∞,-2)上是增函数,
(x2-2ax-3)在(-∞,-2)上是增函数,
首先必有0<a2<1,即0<a<1或-1<a<0,
且有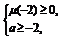 得a≥-
得a≥- .
.
综上,得- ≤a<0或0<a<1.
≤a<0或0<a<1.
9.已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)图象上任意一点P关于原点对称点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
解 (1)设P(x,y)为g(x)图象上任意一点,
则Q(-x,-y)是点P关于原点的对称点,
∵Q(-x,-y)在f(x)的图象上,
∴-y=loga(-x+1),即y=g(x)=-loga(1-x).
(2)f(x)+g(x)≥m,即loga ≥m.
≥m.
设F(x)=loga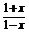 ,x∈[0,1),
,x∈[0,1),
由题意知,只要F(x)min≥m即可.
∵F(x)在[0,1)上是增函数,
∴F(x)min=F(0)=0.故m≤0即为所求.
8.若a2>b>a>1,则logb ,logab,logba从小到大的依次排列为 .
,logab,logba从小到大的依次排列为 .
答案?logb <logba<logab
<logba<logab
7.(2008·青岛质检)计算(log3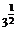 )2-
)2- +log0.25
+log0.25 +9log5
+9log5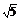 -log
-log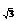 1= .
1= .
答案 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com