
120. 矩形ABCD,AB=3,BC=4,沿对角线BD把△ABD折起,使点A在平面BCD上的射影A′落在BC上,求二面角A-BD-C的大小的余弦值.
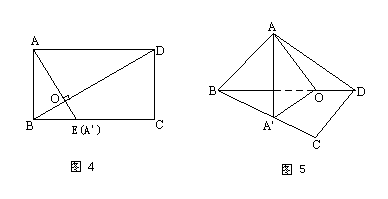
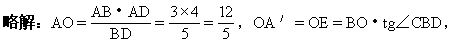

在Rt△AA′O中,∠AA′O=90°,


119. 正方体ABCD-A1B1C1D1中,E、F分别是BB1,CC1的中点,求异面直线AE和BF所成
角的大小.
解析:取DD1的中点G,可证四边形ABFG是平行四边形,得出BF∥AG,
则∠GAE是异面直线AE与BF所成的角.连GF,设正方体棱长为a,

 ,
, .
.
在△AEG中,由余弦定理得
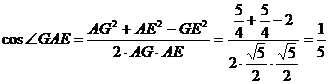
∴  .
.
118. 如图,△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=
 ∠DBC=120°,求
∠DBC=120°,求
(1) A、D连线和直线BC所成角的大小;
(2) 二面角A-BD-C的大小
解析:在平面ADC内作AH⊥BC,H是垂足,连HD.因为平面ABC⊥平面BDC.所以AH⊥平面BDC.HD是AD在平面BDC的射影.依题设条件可证得HD⊥BC,由三垂线定理得AD⊥BC,即异面直线AD和BC形成的角为90°.
在平面BDC内作HR⊥BD,R是垂足,连AR.HR是AR在平面BDC的射影,∴ AR⊥BD,∠ARH是二面角A-BD-C的平面角的补角,设AB=a,可得,
 ,
,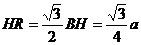 ,
,
∴ 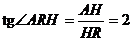 .
.
∴ 二面角A-BD-C的大小为π-arctg2.
117.  已知平面α⊥平面β,交线为AB,C∈
已知平面α⊥平面β,交线为AB,C∈ ,D∈
,D∈ ,
, ,E为BC的中点,AC⊥BD,BD=8.
,E为BC的中点,AC⊥BD,BD=8.
①求证:BD⊥平面 ;
;
②求证:平面AED⊥平面BCD;
③求二面角B-AC-D的正切值.
解析:①AB是AC在平面β上的射影,由AC⊥BD得AB⊥BD.∵ α⊥β.∴ DB⊥α.
②由AB=AC,且E是BC中点,得AE⊥BC,又AE⊥DB,故AE⊥平面BCD,因此可证得平面AED⊥平面BCD.
③设F是AC中点,连BF,DF.由于△ABC是正三角形,故BF⊥AC.又由DB⊥平面α,则DF⊥AC,∠BFD是二面角B-AC-D的平面角,
在Rt△BFD中,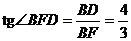 .
.
116. 二面角α-a-β的值为θ(0°<θ<180°),直线l⊥α,判断直线l与平面β的位置关系,并证明你的结论.
解析: 分两种情况,θ=90°,θ≠90°.
当θ=90°时,l∥β或l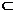 β,这个结论可用反证法证明;
β,这个结论可用反证法证明;
当θ≠90°时,l必与β相交,也可用反证法证明.
115. 两个正方形ABCD和ABEF所在的平面互相垂直,求异面直线AC和BF所成角的大小.
解析:作BP∥AC交DC延长线于P,则∠FBP(或补角)就是异面直线BF和AC所成的角,设正方形边长为a,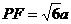 在△BPF中,由余弦定理得
在△BPF中,由余弦定理得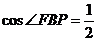 ,异面直线AC和BF成60°角.
,异面直线AC和BF成60°角.
114. 设S为 平面外的一点,SA=SB=SC,
平面外的一点,SA=SB=SC, ,若
,若 ,求证:平面ASC
,求证:平面ASC 平面ABC。
平面ABC。
解析:(1)把角的关系转化为边的关系
(2)利用棱锥的性质(三棱锥的侧棱相等,则顶点在底面上的射影为底面三角形的外心)
证明:设D为AB的中点
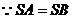


同理
 且
且
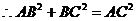
即 为
为 且S在平面上的射影O为
且S在平面上的射影O为 的外心
的外心
则O在斜边AC的中点。
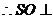 平面ABC
平面ABC
 平面SAC
平面SAC
 平面ASC
平面ASC 平面ABC
平面ABC
113.  已知SA、SB、SC是共点于S的且不共面的三条射线,∠BSA=∠ASC=45°,∠BSC=60°,求证:平面BSA⊥平面SAC
已知SA、SB、SC是共点于S的且不共面的三条射线,∠BSA=∠ASC=45°,∠BSC=60°,求证:平面BSA⊥平面SAC
解析:先作二面角B-SA-C的平面角,根据给定的条件,在棱S上取一点P,分别是在两个平面内作直线与棱垂直
证明:在SA上取一点P
过P作PR⊥SA交SC于R
过P作PQ⊥SA交SB于Q
∴∠QPR为二面角B-SA-C的平面角设PS=a
∵∠PSQ=45°,∠SPQ=90°
∴PQ=a,SQ= a
a
同理PR=
a,SR=  a
a
∵∠PSQ=60°,SR=SQ= a
a
∴ΔRSQ为正三角形则RQ= a
a
∵PR2+PQ2=2a2=QR2
∴∠QPQ=90°
∴二面角B-SA-C为90°
∴平面BSA⊥平面SAC
122. 如果两个相交平面都垂直于第三个平面,那么它们的交线也垂直于这个平面。
已知:β⊥α,γ⊥α,β γ=a
γ=a

求证:a⊥α
解析:利用线面垂直的性质定理
证明:设α β=AB,α
β=AB,α γ=CD
γ=CD
在平面β内作L1⊥AB,
在平面γ内作L1⊥CD,
∵α⊥β∴L1⊥α
同理L2⊥α
∴L1//L2
∴L1//β
∴L1//a
∴a⊥α
121.  已知如图,P
已知如图,P 平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90 °求证:平面ABC⊥平面PBC
平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90 °求证:平面ABC⊥平面PBC
解析:要证明面面垂直,只要在其呈平面内找一条线,然后证明直线与另一平面垂直即可。显然BC中点D,证明AD垂直平PBC即可
证明: 取BC中点D 连结AD、PD
∵PA=PB;∠APB=60°
∴ΔPAB为正三角形
同理ΔPAC为正三角形
设PA=a
在RTΔBPC中,PB=PC=a
BC= a
a
∴PD=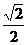 a
a
在ΔABC中
AD=
=
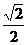 a
a
∵AD2+PD2=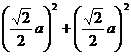
=a2=AP2
∴ΔAPD为直角三角形
即AD⊥DP
又∵AD⊥BC
∴AD⊥平面PBC
∴平面ABC⊥平面PBC
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com