
209. 长方体ABCD-A1B1C1D1中,AB1与A1D所成的角为α,AC与BC1所成的角为β,A1C1与CD1所成的角为γ。 求证:α+β+γ=π
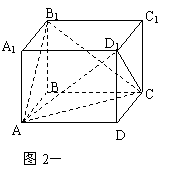 解析:作如图的辅助线
则∠AB1C为AB1与A1D所成的角∠AB1C=α
∵AB
解析:作如图的辅助线
则∠AB1C为AB1与A1D所成的角∠AB1C=α
∵AB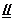 A1B1
A1B1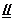 C1D1
∴BC1//AD1,故∠D1AC为AC与BC1所成的角∠D1AC=β
∵AA1
C1D1
∴BC1//AD1,故∠D1AC为AC与BC1所成的角∠D1AC=β
∵AA1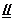 DD1
DD1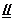 CC1,∴A1C1//AC
∴∠D1CA即为A1C1与CD1所成的角∠D1CA=γ
在△ACD1和△ACB1中,AB1=CD1,B1C=D1A,AC=CA
∴△ACD1≌△CAB1,故∠AB1C=∠AD1C,故∠AD1C=α
在△AD1C中,∠AD1C+∠D1CA+∠D1AC=π
即:α+β+γ=π
CC1,∴A1C1//AC
∴∠D1CA即为A1C1与CD1所成的角∠D1CA=γ
在△ACD1和△ACB1中,AB1=CD1,B1C=D1A,AC=CA
∴△ACD1≌△CAB1,故∠AB1C=∠AD1C,故∠AD1C=α
在△AD1C中,∠AD1C+∠D1CA+∠D1AC=π
即:α+β+γ=π
208. a、b、c为三条不重合的直线,α、β、γ为三个不重合平面,现给出六个命题,
① ②
②  ③
③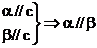 ④
④ ⑤
⑤ 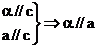 ⑥
⑥ 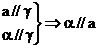 其中正确的命题是( )
A. ①②③ B. ①④⑤ C. ①④
D. ①④⑤⑥
其中正确的命题是( )
A. ①②③ B. ①④⑤ C. ①④
D. ①④⑤⑥
解析: 首先要判断每个命题的真假,错误的命题只需给出一个反例。
解答: ①三线平行公理, ②两直线同时平行于一平面,这二直线可相交,平行或异面 ③二平面同时平行于一直线这两个平面相交或平行
④面面平行传递性,
⑤一直线和一平面同时平行于另一直线,这条直线和平面可平行或直线在平面内,
⑥一直线和一平面同时平行于另一平面,这直线和平面可平行也可能直线在平面内,
故①④正确 ∴应选C。
207. 如图2-33:线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12, ACF的面积为72,求
ACF的面积为72,求 BDE的面积。
BDE的面积。
解析: 求 BDE的面积,看起来似乎与本节内容无关,事实上,已知
BDE的面积,看起来似乎与本节内容无关,事实上,已知 ACF的面积,若
ACF的面积,若 BDE与
BDE与 ACF的对应边有联系的话,可以利用
ACF的对应边有联系的话,可以利用 ACF的面积求出
ACF的面积求出 BDE的面积。
(提示:①
BDE的面积。
(提示:① ABC的两条邻边分别长为a、b,夹角为θ,则
ABC的两条邻边分别长为a、b,夹角为θ,则 ABC的面积S=
ABC的面积S= absinθ,②sinα=sin(180°-α)
absinθ,②sinα=sin(180°-α)
 解答:∵平面QAF∩α=AF,平面QAF∩β=BE,又∵α∥β,∴AF∥BE
同理可证:AC//BD,∴∠FAC与∠EBD相等或互补,即sin∠FAC=
sin∠EBD.
由 AF∥BE,得
解答:∵平面QAF∩α=AF,平面QAF∩β=BE,又∵α∥β,∴AF∥BE
同理可证:AC//BD,∴∠FAC与∠EBD相等或互补,即sin∠FAC=
sin∠EBD.
由 AF∥BE,得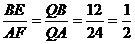 ,∴BE=
,∴BE= AF
由BD//AC,得:
AF
由BD//AC,得: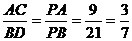 ,∴BD=
,∴BD= AC
又∵
AC
又∵ ACF的面积为72,即
ACF的面积为72,即 AF·AC·sin∠FAC=72,
AF·AC·sin∠FAC=72,
∴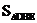 =
= BE·BD·sin∠EBD
=
BE·BD·sin∠EBD
= ·
· AF·
AF· AC·sin∠FAC
=
AC·sin∠FAC
= ·
· AF·AC·sin∠FAC=
AF·AC·sin∠FAC= ×72=84
∴
×72=84
∴ BDE的面积为84平方单位。
BDE的面积为84平方单位。
206. 已知(如图):三棱锥P-ABC中,异面直线PA与BC所成的角为
已知(如图):三棱锥P-ABC中,异面直线PA与BC所成的角为 ,二面角P-BC-A为
,二面角P-BC-A为 ,△PBC和△ABC的面积分别为16和10,BC=4.
,△PBC和△ABC的面积分别为16和10,BC=4.
求:(1)PA的长;(2)三棱柱P-ABC的体积
解析:
(1)作AD⊥BC于D,连PD,由已知PA⊥BC,∴BC⊥面PAD,∴BC⊥PD,∴∠PDA为二面角的平面角,∴∠PDF= ,
,
可算出PD=8,AD=5,∴PA=7;(2)V=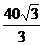
205. 已知正三棱柱ABC-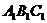 的底面边长为8,侧棱长为6,D为AC中点,
的底面边长为8,侧棱长为6,D为AC中点,
(1)求证:AB1∥平面C1DB;(2)求异面直线AB1与BC1所成角的余弦值.
(1) 解析:连B1C交BC1于E,连结ED,则AB1∥DE,由线面平行定理得AB1∥平面BDC1;(2)∵AB1∥DE,∴DE与BC1所成锐角就是异面直线AB1与BC1所成的角,又BD⊥DC,在Rt△BDC1中,
易知BE=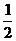 BC1=5,DE=5,BD=
BC1=5,DE=5,BD=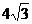 ,在△BDE中,
,在△BDE中, ∠BED=
∠BED= ,∴异面直线AB1与BC1所成角的余弦值为
,∴异面直线AB1与BC1所成角的余弦值为
204. 如图:D、E是是等腰直角三角形ABC中斜边BC的两个三等分点,沿AD和AE将△ABD和△ACE折起,使AB和AC重合,求证:平面ABD⊥平面ABE.
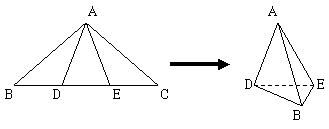
解析:过D作DF⊥AB交AB于F,连结EF,计算DF、EF的长,又DE为已知,三边长满足勾股定理,∴∠DFE=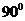 ;
;
203. 在RtΔABC中,AB=BC,E、F分别是AC和AB的中点,以EF为棱把它折成大小为β的二面角A-EF-B后,设∠AEC=α,
求证:2cosα-cosβ=-1.
解析:∠AFB=β.可证:BC⊥AB,然后利用AC2=BC2+AB2即可证得.
202. 正四面体棱长为a,求其内切球与外接球的表面积。
解析:设正四面体的面BCD和面ACD的中心分别为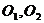 ,连结
,连结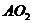 与
与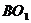 并延长,必交于CD的中点E,又
并延长,必交于CD的中点E,又 ,
,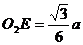 ,连接
,连接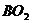 ,在Rt△
,在Rt△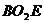 中,
中,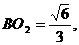 连结
连结 与
与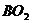 交于
交于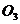 ,由Rt△
,由Rt△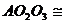 Rt△
Rt△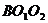 ,∴
,∴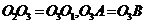 ,同理可证
,同理可证 到另二面的距离也等
到另二面的距离也等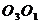 ,
,
∴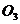 为四面体外接球与内接球的球心,由△
为四面体外接球与内接球的球心,由△ ∽△
∽△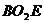 ,∴
,∴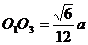 ,
,
∴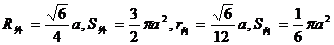
201. .已知过球面上A、B、C三点的截面和球心的距离等于球半径的一半,且AB=BC=AC=2,求球的体积。
解析:过A、B、C三点截面的小圆的半径就是正△ABC的外接圆的半径 ,
,
它是Rt△中 所对的边,其斜边为
所对的边,其斜边为 ,即球的半径为
,即球的半径为 ,∴
,∴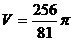 ;
;
200. A、B为球面上相异的两点,则通过A、B可作大圆( )
A.一个 B.无穷多个 C.零个 D.一个或无穷多个
解析:D
当A,B点在球直径上,,这样的大圆有无数个,当不在球直径上,与球心O三个点唯一确定一个平面。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com