
356. 已知平面α∥平面β,B,D∈β,AB⊥CD,且AB=2,直线AB与平面α所成的角为30°,则线段CD的长为取值范围是( )
A.[1,+∞] B.(1,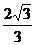 ) C.(
) C.(
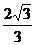 ,
,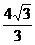 ) D.[
) D.[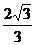 ,+∞)
,+∞)
解析:本题考查直线与直线所成的角,直线与平面所成的角的概念。线面垂直的判定和性质,以及空间想象能力和几何计算.

解 如图所示,过D作DA′∥AB交平面α于A′.由α∥β,故DA′=AB=2,DA′与α成30°角,由已知DC⊥AB,可得DC⊥DA′,所以DC在过DC且与DA′垂直的平面γ内,令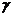 ∩α=l,在
∩α=l,在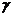 内,DC⊥l时为最短,此时DC=DA′·tan30°=
内,DC⊥l时为最短,此时DC=DA′·tan30°=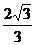 .故CD≥
.故CD≥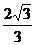 .∴应选D.
.∴应选D.
355. 一张正方形的纸ABCD,BD是对角线,过AB、CD的中点E、F的线段交BD于O,以EF为棱,将正方形的纸折成直二面角,则∠BOD等于( )
A.120° B.150° C.135° D.90°

解析:本题考查线面垂直,面面垂直,余弦定理,以及空间与平面问题的转化能力。
如图,设正方形边长为a,由O为正方形中心,则BO= a,DO=
a,DO= a,连AB,因为DA⊥AE,DA⊥BE,故DA⊥面AEB,所以DA⊥AB,故ΔDAB为直角三角形,BD=
a,连AB,因为DA⊥AE,DA⊥BE,故DA⊥面AEB,所以DA⊥AB,故ΔDAB为直角三角形,BD= =
=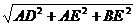 =
= =
= a.
a.
又在ΔBOD中,由余弦定理可得
cos∠BOD= =
= =-
=-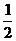 ,所以∠BOD=120°
,所以∠BOD=120°
评析:本题为折叠问题,此类问题应该分清折叠前后的哪些量发生了变化,此外,还要注意找出空间转化为平面的途径,几何计算的准确性等。
354. 已知直线l⊥平面α,直线m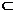 平面β,有下面四个命题:
平面β,有下面四个命题:
(1)α∥β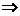 l⊥m (2)α⊥β
l⊥m (2)α⊥β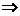 l∥m
l∥m
(3)l∥m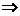 α⊥β (4)l⊥m
α⊥β (4)l⊥m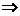 α∥β
α∥β
其中正确的两个命题是( )
A.(1)与(2) B.(3)与(4) C.(2)与(4) D.(1)与(3)
分析:本题主要考查直线与平面、平面和平面的位置关系,以及空间想象能力和逻辑推理能力.
解法一:在l⊥α,m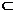 β的前提下,当α∥β时,有l⊥β,从而l⊥β,从而l⊥m,得(1)正确;当α⊥β时,l垂直于α、β的交线,而m不一定与该交线垂直,因此,l与m不一定平行,故(2)不正确.故应排除A、C.依题意,有两个命题正确,不可能(3),(4)都正确,否则连同(1)共有3个命题正确.故排除B,得D.
β的前提下,当α∥β时,有l⊥β,从而l⊥β,从而l⊥m,得(1)正确;当α⊥β时,l垂直于α、β的交线,而m不一定与该交线垂直,因此,l与m不一定平行,故(2)不正确.故应排除A、C.依题意,有两个命题正确,不可能(3),(4)都正确,否则连同(1)共有3个命题正确.故排除B,得D.
解法二:当断定(1)正确之后,根据4个选择项的安排,可转而检查(3),由l∥m,l∥α知m⊥α,从而由m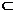 α得α⊥β.即(3)正确.故选D.
α得α⊥β.即(3)正确.故选D.
解法三:不从(1)检查起,而从(2)、(3)、(4)中任一命题检查起,如首先检查(4);由l⊥α,m⊥β不能否定m是α、β的交线,因此α∥β不一定成立,故(4)是不正确的,因此可排除B、C.依据A和D的内容可知(1)必定是正确的,否则A和D也都排除,以下只要对(2)或(3)检查,只须检查一个便可以做出判断.
353. 如图9-50,点A在锐二面角a -MN-b 的棱MN上,在面a 内引射线AP,使AP与MN所成的∠PAM为45°,与面b 所成的角为30°,求二面角a -MN-b 的大小.
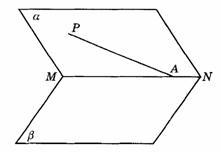
解析:如图答9-44,取AP上一点B,作BH⊥b 于H,连结AH,则∠BAH为射线AP与平面b 所成的角,∴ ∠BAH=30°,再作BQ⊥MN,交MN于Q,连结HQ,则HQ为BQ在平面b 内的射影.由三垂线定理的逆定理,HQ⊥MN,∴ ∠BQH为二面角a -MN-b 的平面角.

图答9-44
设BQ=a,在Rt△BAQ中,∠BQA=90°,∠BAM=45°,∴ 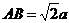 ,在Rt△BAH中∠BHA=90°,∠BAH=30°,∴
,在Rt△BAH中∠BHA=90°,∠BAH=30°,∴  .在Rt△BHQ中,∠BHQ=90°,BQ=a,
.在Rt△BHQ中,∠BHQ=90°,BQ=a, ,
,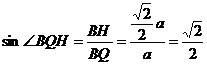 ,∵ ∠BQH是锐角,∴ ∠BQH=45
,∵ ∠BQH是锐角,∴ ∠BQH=45
即二面角a -MN-b 等于45°.
352. 在正方体 中,求二面角
中,求二面角 的大小.
的大小.
解析:如图9-43,在平面 内作
内作 ,交
,交 于E.连结
于E.连结 ,设正方体棱长为a,在△
,设正方体棱长为a,在△ 和△
和△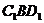 中,
中,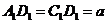 ,
,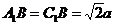 ,
,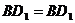
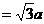 ,∴ △
,∴ △ ≌△
≌△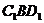 ,∵
,∵  ,∴
,∴  ,∴
,∴ 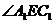 为二面角
为二面角 的平面角.在Rt△
的平面角.在Rt△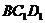 中,
中, ,∴
,∴ 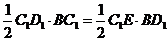 ,∴
,∴  ,在△
,在△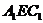 中,
中,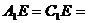

 ,
, ,
, ,
,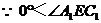
 ,
,
351. (1)已知直线a∥平面a ,a⊥平面b .求证:b ⊥a .
(2)已知三个平面a 、b 、g ,a ∥b ,a ⊥g .求证:b ⊥g .
解析:(1)如图答9-41,∵ a∥a
,∴ 在a 上任取一点 ,过a与A确定平面g ,设
,过a与A确定平面g ,设 ,则
,则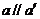 .∵ a⊥b
,∴
.∵ a⊥b
,∴  .∵
.∵ 
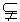 a ,∴ a ⊥b
.
a ,∴ a ⊥b
.
(2)在g
上任取P,设 ,在g 内作
,在g 内作 ,∵ a ⊥g ,∴ PQ⊥a .∵ a
∥b ,∴ PQ⊥b
,∵ PQ
,∵ a ⊥g ,∴ PQ⊥a .∵ a
∥b ,∴ PQ⊥b
,∵ PQ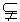 g ,∴ b ⊥g
.
g ,∴ b ⊥g
.
350. 如图9-46,二面角a -AB-b 的棱AB上有一点C,线段CD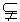 a ,CD=100,∠BCD=30°,点D到平面b 的距离为
a ,CD=100,∠BCD=30°,点D到平面b 的距离为 ,则二面角a -AB-b
的度数是________.
,则二面角a -AB-b
的度数是________.
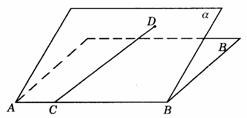
解析:60°.作DH⊥b 于H,DE⊥AB于E,连结EH,则EH是DE在平面b 内的射影.由三垂线定理的逆定理,HE⊥AB,∴ ∠DEH为二面角a
-AB-b 的平面角.在Rt△DCE中,CD=100,∠BCD=30°,∴ DE=CDsin30°=50,在Rt△DEH中, ,
,
 ∴ ∠DEH=60°,即二面角a
-AB-b 等于60°.
∴ ∠DEH=60°,即二面角a
-AB-b 等于60°.

349. 立体图形A-BCD中,AB=BC=CD=DB=AC=AD,相邻两个面所成的二面角的平面角为q ,则( ).
A.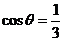 B.
B. C.
C. D.
D.
解析:A.任取一个二面角,如A-BC-D,取BC中点E,可证AE⊥BC,DE⊥BC,∴
∠AED是二面角A-BC-D的平面角,设AB=1,则

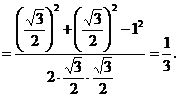
348.
正方体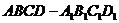 中,二面角
中,二面角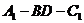 的大小的余弦值为( ).
的大小的余弦值为( ).
A.0 B.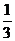 C.
C.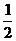 D.
D.
解析:B.取BD中点O,连结 、
、 ,则
,则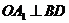 ,
,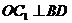 ,∴
,∴  为二面角
为二面角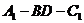 的平面角,设为q ,设正方体棱长为a,则
的平面角,设为q ,设正方体棱长为a,则 ,
,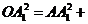
 ∴
∴ 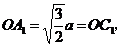
∴ 
347. 线段AB长为2a,两端点A、B分别在一个直二面角的两个面上,AB和两个面所成的角为45°和30°,那么A、B在棱上的射影间的距离为( ).
A.2a B.a C. D.
D.
解析:B.如图答9-39,设直二面角为a -l-b ,作AC⊥l于C,BD⊥l于D,则AC⊥b ,BD⊥a ,连结AD、BC,∴ ∠ABC为AB与b 所成的角,∠BAD为AB与a 所成的角,∴
∠ABC=30°,∠BAD=45°,∵ AB=2a,∴ AC=a,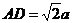 .在Rt△ACD中,
.在Rt△ACD中,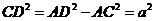 ,∴ CD=a.
,∴ CD=a.

图答9-39
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com