
416. 空间可以确定一个平面的条件是( )
A.两条直线 B.一点和一直线
C.一个三角形 D.三个点
解析: 由推论2和推论3知两条相交直线或者两条平行直线才确定一个平面,两条直线还有位置关系异面.故排除A,由推论1知点必在线外才合适,排除B.由公理3知不共线三点可确定一个平面,D中三个点不一定不共线,排除D.公理3结合公理1,知选C.
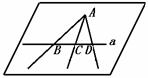
415.过已知直线外一点与这条直线上的三点分别画三条直线,证明:这三条直线在同一平面内.
解答:已知:A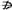 a,如图,B、C、D∈a,证明:AB、AC、AD共面.
a,如图,B、C、D∈a,证明:AB、AC、AD共面.
证明:∵A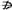 a,∴A,a确定平面α,∵B、C、D∈a,a
a,∴A,a确定平面α,∵B、C、D∈a,a α.
α.
∴B、C、D∈α
又A∈α.
∴AB、AC、AD α.
α.
即AB、AC、AD共面.
414.一条直线过平面内一点与平面外一点,它和这个平面有几个公共点?为什么?
解析:只有一个,假设有两个公共点,由公理1知该直线上所有点都在这个平面内,这和直线过平面外一点矛盾.
413. 证明推论3成立.(如图)

已知:a∥b,求证:经过a,b的平面有且只有一个.
证明:(存在性)∵a∥b,由平行线的定义知:a、b共面,所以经过a、b的平面有一个.
(唯一性),在a上取两点A、B,在b上取一点C.
∵a∥b,∴A、B、C三点不共线,由公理3知过A、B、C三点的平面只有一个,从而过a,b两直线的平面也是惟一的.
412. 证明两两相交而不共点的四条直线在同一平面内.
已知:如图,直线l1,l2,l3,l4两两相交,且不共点.
求证:直线l1,l2,l3,l4在同一平面内

解析:证明几条直线共面的依据是公理3及推论和公理1.先证某两线确定平面α,然后证其它直线也在α内.
证明:图①中,l1∩l2=P,
∴ l1,l2确定平面α.
又 l1∩l3=A,l2∩l3=C, ∴ C,A∈α.
故 l3 α.
α.
同理 l4 α.
α.
∴ l1,l2,l3,l4共面.
图②中,l1,l2,l3,l4的位置关系,同理可证l1,l2,l3,l4共面.
所以结论成立.
411. 直线m、n分别和平行直线a、b、c都相交,交点为A、B、C、D、E、F,如图,求证:直线a、b、c、m、n共面.

解析: 证明若干条直线共面的方法有两类:一是先确定一个平面,证明其余的直线在这个平面里;二是分别确定几个平面,然后证明这些平面重合.
证明 ∵a∥b,∴过a、b可以确定一个平面α.
∵A∈a,a α,∴A∈α,同理B∈a.
α,∴A∈α,同理B∈a.
又∵A∈m,B∈m,∴m α.同理可证n
α.同理可证n α.
α.
∵b∥c,∴过b,c可以确定平面β,同理可证m β.
β.
∵平面α、β都经过相交直线b、m,
∴平面α和平面β重合,即直线a、b、c、m、n共面.
410. 点P、Q、R分别在三棱锥A-BCD的三条侧棱上,且PQ∩BC=X,QR∩CD=Z,PR∩BD=Y.求证:X、Y、Z三点共线.

解析: 证明点共线的基本方法是利用公理2,证明这些点是两个平面的公共点.
证明 ∵P、Q、R三点不共线,∴P、Q、R三点可以确定一个平面α.
∵ X∈PQ,PQ α,∴X∈α,又X∈BC,BC
α,∴X∈α,又X∈BC,BC 面BCD,∴X∈平面BCD.
面BCD,∴X∈平面BCD.
∴ 点X是平面α和平面BCD的公共点.同理可证,点Y、Z都是这两个平面的公共点,即点X、Y、Z都在平面α和平面BCD的交线上.
409. 若ΔABC所在的平面和ΔA1B1C1所在平面相交,并且直线AA1、BB1、CC1相交于一点O,求证:
(1)AB和A1B1、BC和B1C1、AC和A1C1分别在同一平面内;
(2)如果AB和A1B1、BC和B1C1、AC和A1C1分别相交,那么交点在同一直线上(如图).

(1)证明:∵AA1∩BB1=O,
∴AA1、BB1确定平面BAO,
∵A、A1、B、B1都在平面ABO内,
∴AB 平面ABO;A1B1
平面ABO;A1B1 平面ABO.
平面ABO.
同理可证,BC和B1C1、AC和A1C1分别在同一平面内.
(2)分析:欲证两直线的交点在一条直线上,可根据公理2,证明这两条直线分别在两个相交平面内,那么,它们的交点就在这两个平面的交线上.
证明:如图,设AB∩A1B1=P;
AC∩A1C1=R;
∴ 面ABC∩面A1B1C1=PR.
∵ BC 面ABC;B1C1
面ABC;B1C1 面A1B1C1,
面A1B1C1,
且 BC∩B1C1=Q ∴ Q∈PR,
即 P、R、Q在同一直线上.
408. 已知四棱锥P-ABCD,它的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,又PC=a,E为PA的中点.
(1)求证:平面EBD⊥平面ABCD;
(2)求点E到平面PBC的距离;
(3)求二面角A-BE-D的大小.

(1)证明: 在四棱锥P-ABCD中,底面是菱形,连结AC、BD,交于F,则F为AC的中点.
又E为AD的中点,∴EF∥PC
又∵PC⊥平面ABCD,∴EF⊥平面ABCD.EF 平面EBD.
平面EBD.
∴平面EBD⊥平面ABCD.
(2)∵EF∥PC,∴EF∥平面PBC
∴E到平面PBC的距离即是EF到平面PBC的距离
过F作FH⊥BC交BC于H,
∵PC⊥平面ABCD,FH 平面ABCD
平面ABCD
∴PC⊥FH.
又BC⊥FH,∴FH⊥平面PBC,则FH是F到平面PBC的距离,也是E到平面PBC的距离.
∵∠FCH=30°,CF=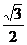 a.
a.
∴FH= CF=
CF=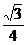 a.
a.
(3)取BE的中点G,连接FG、AG由(1)的结论,平面BDE⊥平面ABCD,AF⊥BD,
∴AF⊥平面BDC.
∵BF=EF=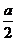 ,∴FG⊥BE,由三垂线定理得,AG⊥BE,
,∴FG⊥BE,由三垂线定理得,AG⊥BE,
∴∠FGA为二面角D-BE-A的平面角.
FG=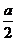 ×
×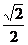 =
= a,AF=
a,AF=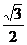 a.
a.
∴tg∠FGA=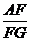 =
=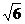 ,∠FAG=arctg
,∠FAG=arctg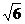
即二面角A-BE-D的大小为arctg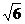
407. 如图,在三棱柱ABC-A′B′C′中,四边形A′ABB′是菱形,四边形BCC′B′是矩形,C′B′⊥AB.
(1)求证:平面CA′B⊥平面A′AB;
(2)若C′B′=2,AB=4,∠ABB′=60°,求AC′与平面BCC′B′所成角的大小.(用反三角函数表示)

解析:(1)∵在三棱柱ABC-A′B′C中,C′B′∥CB,∴CB⊥AB.∵CB⊥BB′,AB∩BB′=B,∴CB⊥平面A′AB.∵CB 平面CA′B,∴平面CA′B⊥平面A′AB
平面CA′B,∴平面CA′B⊥平面A′AB
(2)由四边形A′ABB′是菱形,∠ABB′=60°,连AB′,可知ΔABB′是正三角形.取 B B′中点H,连结AH,则AH⊥BB′.又由C′B′⊥平面A′AB,得平面A′ABB′⊥平面
C′B′BC,而AH垂直于两平面交线BB′,∴AH⊥平面C′B′BC.连结C′H,则∠AC′H为 AC′与平面BCC′B′所成的角,AB′=4,AH=2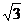 ,于是直角三角形C′B′A中,A′C=5,在RtΔAHC′中,sin∠AC′H=
,于是直角三角形C′B′A中,A′C=5,在RtΔAHC′中,sin∠AC′H= ∴∠AC′H=arcsin
∴∠AC′H=arcsin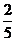
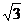 ,∴直线AC′与平面BCC′B′所成的角是arcsin
,∴直线AC′与平面BCC′B′所成的角是arcsin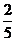
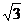 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com