
455. 如图,平行六面体ABCD-A1B1C1D1的底面是边长为1的正方形,侧棱AA1长为2,且∠A1AB=∠A1AD=60°则此平行六面体的体积为
解析:一 求平行六面体ABCD-A1B1C1D的体积,应用公式.由于底面是正方形,所以关键是求高,即 到底面ABCD的距离
到底面ABCD的距离
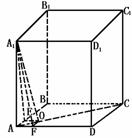
解法一:过点A1做A1O⊥平面ABCD,垂足为O,过O做OE⊥AB,OF⊥AD,垂足分别为E、F,连结A1E,A1F,可知O在∠BAD的平分线AC上.
∴cos∠A1AO·cos∠OAF=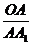 ·
·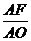 =
= =cos∠A1AF
=cos∠A1AF
即cos∠A1AO·cos45°=cos60°
∴cos∠A1AO=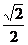
∴sin∠A1AO=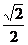
∴A1O=A1Asin∠A1AO=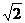
∴V=SABCD·A1O=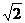
分析二 如图,平行六面体的对角面B1D1DB把平行六面体分割成两个斜三棱柱,它们等底面积、等高、体积相等,考察其中之一三棱柱A1B1D1-ABD.
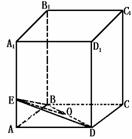
解法二:过B作BE⊥A1A,连结DE,可知面BDE是其直截面,把斜三棱柱分割成上下两部分,若把两部分重新组合,让面A1D1B1与面ADB重合,则得到一直棱柱,ΔBDE是其底面,DD1是其侧棱,并且和斜三棱柱A1B1D1-ABD的体积相等.
取BD中点O,连结OE,易知
SΔBED= BD·OE=
BD·OE= BD·
BD·
= ·
·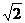 ·
·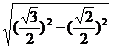 =
=
∴V直棱柱=SΔDEB·DD1
= ×2=
×2=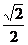 =
=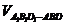
∴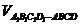 =2
=2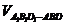 =
=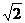
点评 在解决体积问题时,“割”“补”是常用的手段,另外本题分析二给出了求斜棱柱体积的另一方法:斜棱柱的体积=直截面面积×侧棱长.
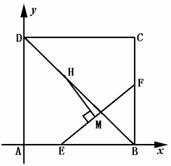
454. 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E、F分别在棱AB、BC上,G在对角线BD1上,且AE=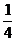 ,BF=
,BF= ,D1G∶GB=1∶2,求平面EFG与底面ABCD所成的二面角的大小.
,D1G∶GB=1∶2,求平面EFG与底面ABCD所成的二面角的大小.
解析:设G在底面ABCD上的射影为H,H∈BD,
∵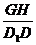 =
= =
=
∴GH=
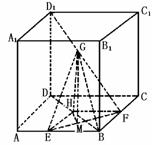
作HM⊥EF于M,连GM,由三垂线定理知GM⊥EF,则∠GMH=θ就是平面BFG与底面ABCD所成的二面角的平面角,tanθ=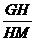 .
.
下面求HM的值.
建立如图所示的直角坐标系,据题设可知.
H( ,
, )、E(
)、E(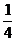 ,0)、F(1,
,0)、F(1, )
)
∴直线EF的方程为
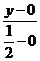 =
=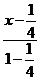 ,
,
即 4x-6y-1=0.
由点到直线的距离公式可得
|HM|= =
=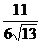 ,
,
∴tgθ= ·
· =
= ,θ=arctg
,θ=arctg .
.
说明 运用解析法来求HM的值是本例的巧妙所在.
453. 在棱长为1的正方体ABCD-A1B1C1D1中,P是A1B1上的一动点,平面PAD1和平面PBC1与对角面ABC1D1所成的二面角的平面角分别为α、β,试求α+β的最大值和最小值.
解析:如图.对角面A1B1CD⊥对角面ABC1D1,其交线为EF.过P作PQ⊥EF于Q,则PQ⊥对角面ABC1D1.分别连PE、PF.
∵EF⊥AD1,PE⊥AD1(三垂线定理).故由二面角的平面角定义知 ∠PFQ=α,

同理,∠PFQ=β.
设A1P=x,(0≤x≤1),则PB1=1-x.
∵EQ=A1P,QF=PB1,PQ=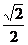 ,
,
∴当0<x<1时,有
tanα= ,tanβ=
,tanβ= ,
,
∴tan(α+β)=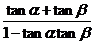 =
=
=
而当x=0时α=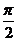 ,tan(α+β)=tan(
,tan(α+β)=tan(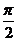 +β)=-cotβ=-
+β)=-cotβ=-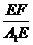 =-
=-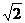 ,上式仍成立;类似地可以验证.当x=1时,上式也成立,于是,当x=
,上式仍成立;类似地可以验证.当x=1时,上式也成立,于是,当x= 时,tan(α+β)取最小值-2
时,tan(α+β)取最小值-2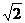 ;当x=0或1时,tan(α+β)取最大值-
;当x=0或1时,tan(α+β)取最大值-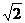 .
.
又∵ 0<α+β<π,
∴(α+β)max=π-arctan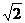
(α+β)min=π-arctan2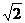
452. 求棱长为a的正方体ABCD-A1B1C1D1的面对角线A1C1与AB1的距离.

解法一:连结BD1,取A1B1的中点E,连BE交AB1于M,连D1E交A1C1于N,连MN.
因为ΔA1NE∽ΔC1ND1,所以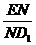 =
=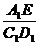 =
= ,
,
则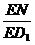 =
= ,同理
,同理 =
= .
.
∵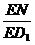 =
= .∴MN∥BD1.
.∴MN∥BD1.
由三垂线定理知BD1与A1C1、AB1都垂直,故MN为两对角线的公垂线,
又ΔEMN∽ΔEBD1
故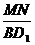 =
=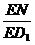 =
= .∴MN=
.∴MN=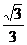 a.
a.
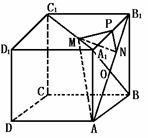
解法二:取A1M= ,B1N=
,B1N= ,过N作NP⊥A1B1于P,连MP,则ΔMPN为直角三角形,由计算,PM=
,过N作NP⊥A1B1于P,连MP,则ΔMPN为直角三角形,由计算,PM= a,PN=
a,PN= a,故MN=
a,故MN=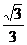 a.又A1N=
a.又A1N=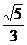 a,A1M=
a,A1M= a,故A1N2=A1M2+MN2,于是MN⊥A1C1;同理,由AN=
a,故A1N2=A1M2+MN2,于是MN⊥A1C1;同理,由AN=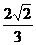 a,AM=
a,AM= a,MN=
a,MN=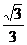 a可知MN⊥AB1.故MN为AB1与A1C1的公垂线段,从而AB1与A1C1的距离为
a可知MN⊥AB1.故MN为AB1与A1C1的公垂线段,从而AB1与A1C1的距离为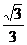 a.
a.
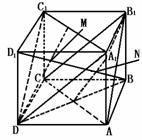
解法三:可转化为求平行平面间的距离.连A1D,C1D,A1C1,B1C.易知A1D∥B1C,A1C1∥AC.故平面A1DC1∥平面AB1C.连BD1,设与平面A1DC1交于M,与平面AB1C交于N.因BD1与图中所示6条面对角线都垂直,故BD⊥面A1DC1,也垂直于AB1C.即MN是A1C1与AB1的距离,在RtΔD1DB中,D1M= =
=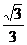 a,而同理可求BN=
a,而同理可求BN=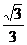 a,故
a,故
MN=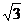 a-
a-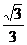 a-
a-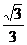 a=
a=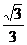 a.
a.
说明 上例还可以利用直线与平面平行、体积转换等方法求解.
451. 如图1,线段AB 平面α,线段CD
平面α,线段CD 平面β,且平面α∥平面β,AB⊥CD,AB=CD=a,α、β的距离为h,求四面体ABCD的体积.
平面β,且平面α∥平面β,AB⊥CD,AB=CD=a,α、β的距离为h,求四面体ABCD的体积.

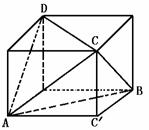
图1 图2
解析:依题意可构造一个底面对角线长为a,高为h的正四棱柱(如图2).
显然,正四棱柱的底面边长为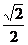 a.其体积为
a.其体积为
V柱=(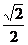 a)2h=
a)2h= a2h.
a2h.
而三棱锥C-AC′B的体积为
V锥=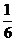 V柱.
V柱.
故四面体ABCD的体积为
V=V柱-4V锥=V柱-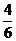 V柱
V柱
= V柱=
V柱=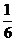 a2h.
a2h.
说明 本题运用了“构造辅助体”的解题技巧.
450. 四面体对棱长分别相等,分别是a,b,c.求体积.

解析: 把四面体“嵌入”棱长为x,y,z的长方体(如图).其充分条件是

有实数解
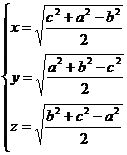
如果关于x,y,z的方程组有实数解,则四面体体积
V=xyz-4· ·(
·( xy)·z=
xy)·z= xyz
xyz
=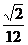

说明 对棱相等的四面体各面是全等的锐角三角形,本题采用了体积分割法,转化法求体积.
449. PA、PB、PC是从点P出发的三条射线,每两条射线的夹角为60°,求直线PC与平面PAB所成的角的余弦值.
解析:如图答9-22,在PC上任取一点D,作DH⊥平面PAB于H,则∠DPH为PC与平面PAB所成的角.作HE⊥PA于E,HF⊥PB于F,连结PH,DE,DF.∵ EH、FH分别为DE、DF在平面PAB内的射影,由三垂线定理可得DE⊥PA.DF⊥PB.∵
∠DPE=∠DPF,∴ △DPE≌△DPF.∴ PE=PF.∴
Rt△HPE≌Rt△HPF,∴
HE=HF,∴ PH是∠APB的平分线.设EH=a,则PH=2EH=2a,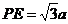 .在Rt△PDE中,∠DPE=60°,DE⊥PA,∴
.在Rt△PDE中,∠DPE=60°,DE⊥PA,∴
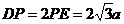 .在Rt△DPH中,DH⊥HP,PH=2a,
.在Rt△DPH中,DH⊥HP,PH=2a,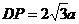 ,∴
,∴ 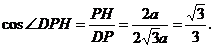

448. 如图9-32,△ABD和△ACD都是以D为直角顶点的直角三角形,且AD=BD=CD,∠BAC=60°.求证:
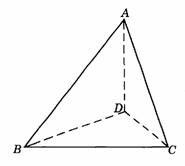
图9-32
(1)BD⊥平面ADC;
(2)若H是△ABC的垂心,则H为D在平面ABC内的射影.
解析:(1)设AD=BD=CD=a,则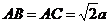 .∵ ∠BAC=60°,∴
.∵ ∠BAC=60°,∴
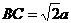 .由勾股定理可知,∠BDC=90°.即BD⊥DC,又∵
BD⊥AD,AD∩DC=D,∴
BD⊥平面ADC.
.由勾股定理可知,∠BDC=90°.即BD⊥DC,又∵
BD⊥AD,AD∩DC=D,∴
BD⊥平面ADC.
(2)如图答9-21,要证H是D在平面ABC上的射影,只需证DH⊥平面ABD.连结HA、HB、HC.∵
H是△ABC的垂心,∴
CH⊥AB.∵
CD⊥DA,CD⊥BD,∴
CD⊥平面ABD,∴ CD⊥AB.∵
CH∩CD=C,∴ AB⊥平面DCH.
∵ DH 平面DCH,∴ AB⊥DH,即DH⊥AB,同理DH⊥BC.∵
AB∩BC=B,∴ DH⊥平面ABC.
平面DCH,∴ AB⊥DH,即DH⊥AB,同理DH⊥BC.∵
AB∩BC=B,∴ DH⊥平面ABC.

447. 如图9-31,SA、SB、SC三条直线两两垂直,点H是S在平面ABC上的射影,求证:H是△ABC的垂心.
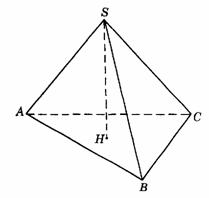
解析:∵ SC⊥SA,SC⊥SB,且SA∩SB=S,∴ SC⊥平面SAB,∴ AB⊥SC.∵ H是S在平面ABC上的射影,∴ SH⊥平面ABC.连结CH,CH为SC在平面ABC上的射影,∵ AB⊥SC,由三垂线定理的逆定理可知CH⊥AB,即CH为AB的垂线.同理AH⊥BC,即AH为BC边的垂线.H为△ABC两条垂线的交点,∴ H为△ABC垂心.
446. 如图9-30,直线a、b是异面直线,它们所成角为30°, 为a、b的公垂线段,
为a、b的公垂线段, .另有B在直线a上,且BA=2cm,求点B到直线b的距离.
.另有B在直线a上,且BA=2cm,求点B到直线b的距离.
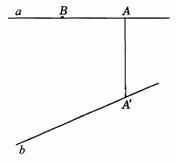
解析:如图答9-20,过 作
作 ,则
,则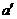 与b确定平面a .作
与b确定平面a .作 于C,在平面a 内作CD⊥b于D,连结BD.∵
于C,在平面a 内作CD⊥b于D,连结BD.∵
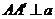 ∴
∴ 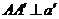 . ∵
. ∵ 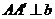 ,
,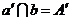 ,∴
,∴ 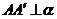 .∵
.∵ 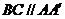 ,∴ BC⊥a .∵ CD⊥b,∴
BD⊥b(三垂线定理),即BD为B点到b的距离.∵
,∴ BC⊥a .∵ CD⊥b,∴
BD⊥b(三垂线定理),即BD为B点到b的距离.∵  ,∴
,∴ 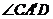 为异面直线a与b所成的角,∴
为异面直线a与b所成的角,∴  .∵
.∵ 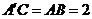 ,
, ,∴ CD=1.在Rt△BCD中,
,∴ CD=1.在Rt△BCD中, ,CD=1,∠BCD=90°,∴
,CD=1,∠BCD=90°,∴ 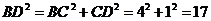 ,∴
,∴  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com