
465. 如图9-52,A是△BCD所在平面外一点,AB=AD,∠ABC=∠ADC=90°,则二面角A-BD-C的平面角是( ).
A.钝角 B.直角
C.锐角 D.大小不确定的

解析:A.取BD中点E,连结AE、CE,由AB=AD,∠ABC=∠ADC,AC=AC得△ABC≌△ADC,∴ DC=BC,∴ AE⊥BD,CE ⊥
BD,∴ ∠AEC为二面角A-BD-C的平面角.∵ 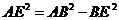 ,
, ,
,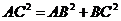 ,∴
,∴ 
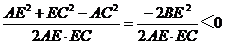 ,∵ ∠AEC为钝角
,∵ ∠AEC为钝角
464. 一条线段的两个端点分别在一个直二面角的两个面内(都不在棱上),则这条线段与这两个平面所成的角的和( ).
A.等于90° B.大于90°
C.不大于90° D.不小于90°
解析:C.如图答9-45,设直二面角a -l-b ,作AC⊥l于C,BD⊥l于D.∵ a ⊥b ,则AC⊥b ,BD⊥a ,连结BC、AD,则∠ABC为AB与平面b 所成的角,∠BAD为AB与平面a 所成的角.
当AB⊥l时,易得AB与a 、b
所成角之和等于90°,当AB与l不垂直时,设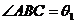 ,
,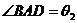 ,
, ,
,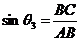 ,
,  ,∵ BC>BD,∴
,∵ BC>BD,∴  ,∵ 函数y=sinx在
,∵ 函数y=sinx在 上是增函数,∴
上是增函数,∴ 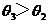 ,∵
,∵ 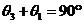 ,∴
,∴ 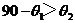 ,∴
,∴ 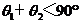 .故AB与a
、b 所成角之和≤90°.
.故AB与a
、b 所成角之和≤90°.

463. 设直线l、m,平面a
、b 、g 满足b
∩g =l,l∥a
,m a ,且m⊥g
,则必有( ).
a ,且m⊥g
,则必有( ).
A.a ⊥g ,且l⊥m B.a ⊥g ,且m∥b
C.m∥b ,且l⊥m D.a ∥b ,且a ⊥g
解析:A.

462. 如图9-51,已知ABCD、ABEF、CDFE都是长方形,且平面ABCD⊥平面ABEF.记∠FCE=q ,∠CFB=a ,∠CEB=b ,则有( ).
A.sinb =sina ·sinq B.cosa =cosb ·cosq
C.sina =sinb ·cosq D.sinb =sina ·cosq

解析:C.
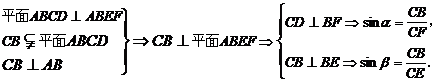
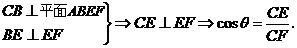
于是sina =sinb ·cosq .
461. 如图,设ABC-A1B1C1是直三棱柱,E、F分别为AB、A1B1的中点,且AB=2AA1=2a,AC=BC=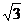 a.
a.
(1)求证:AF⊥A1C
(2)求二面角C-AF-B的大小

分析 本小题考查空间几何垂直的概念和二面角的度量等知识.
解 (1)∵AC=BC,E为AB中点,∴CE⊥AB
又∵ABC-A1B1C1为直棱柱,∴CE⊥面AA1BB
连结EF,由于AB=2AA1
∴AA1FE为正方形
∴AF⊥A1E,从而AF⊥A1C
(2)设AF与A1E交于O,连结CO,由于AF⊥A1E,知AF⊥面CEA1
∴∠COE即为二面角C-AF-B的平面角
∵AB=2AA1=2a,AC=BC=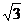 a
a
∴CE=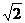 a,OE=
a,OE=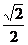 a,∴tan∠COE=
a,∴tan∠COE= =2.
=2.
∴二面角C-AF-B的大小是arctan2.
460. 如图,在正方体ABDC-A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)证明AD⊥D1F
(2)求AE与D1F所成的角
(3)证明面AED⊥面A1FD1
(4)设AA1=2,求三棱锥F-A1ED1的体积V??F-A1ED1?
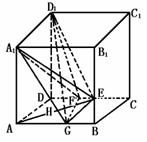
解析:(1)∵AC1是正方体,∴AD⊥面DC1.又D1F DC1,∴AD⊥D1F.
DC1,∴AD⊥D1F.
(2)取AB中点G,连结A1G、FG(如图).因为F是CD的中点,所以GF、AD平行且相等,又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,A1G∥D1F.
设A1G与AE相交于点H,则∠AHA1是AE与D1F所成的角.因为E是BB1的中点,RtΔA1AG≌RtΔABE,∠GA1A=∠GAH,从而∠AHA1=90°,即直线AE与D1F所成角为直角.
(3)由(1)知AD⊥D1F,由(2)知AE⊥D1F,又AD∩AE=A,所以D1F⊥面AED.又因为D1F 面A1ED1,∴体积
面A1ED1,∴体积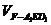 =
= =
=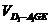 ,∵AA1=2,∴面积
,∵AA1=2,∴面积 =
=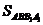 -2
-2 -
- =
= .
.
∴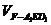 =
= ×A1D1×
×A1D1× =
= ×2×
×2× =1.
=1.
459. 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
(1)求截面EAC的面积
(2)求异面直线A1B1与AC之间的距离
(3)求三棱锥B1-EAC的体积
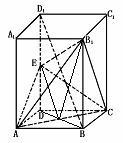
解析:(1)连结DB交AC于O,连结EO.
∵底面ABCD是正方形
∴DO⊥AC
又∵ED⊥底面AC ∴EO⊥AC
∴∠EOD是面EAC与底面AC所成二面角的平面角
∴∠EOD=45°
DO=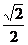 a,AC=
a,AC=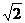 a,EO=
a,EO=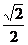 a·sec45°=a.
a·sec45°=a.
故 SΔEAC=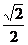 a2.
a2.
(2)解:由题设ABCD-A1B1C1D1是正四棱柱,得A1A⊥底面AC,A1A⊥AC.
又A1A⊥A1B1
∴A1A是异面直线A1B1与AC间的公垂线
∵D1B∥面EAC,且面D1BD与面EAC交线为EO
∴D1B∥EO
又O是DB的中点
∴E是D1D的中点,D1B=2EO=2a.
∴D1D= =
=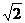 a.
a.
异面直线A1B1与AC间的距离为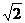 a.
a.
连结B1O,则 =2
=2
∵AO⊥面BDD1B1
∴AO是三棱锥A-EOB1的高,AO=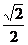 a.
a.
在正方形BDD1B1中,E、O分别是D1D、DB的中点
则: =
= a2.
a2.
∴ =2·
=2· ·
· a2·
a2·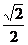 a=
a= a3
a3
所以三棱锥B1-EAC的体积是 a3.
a3.
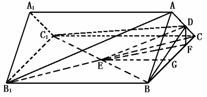
458. 如图,已知A1B1C1-ABC是正三棱柱,D是AC中点.
(1)证明AB1∥面DBC1
(2)假设AB1⊥BC1,BC=2,求线段AB1在侧面BB1CC1上的射影长.
分析:弄清楚正三棱柱的概念,利用三垂线定理找二面角.
解析:(1)证明:∵A1B1C1-ABC是正三棱柱,
∴四形B1BCC1是矩形,连结B1C,交BC1于E,
则B1E=EC,连结DE.
在ΔAB1C中,AD=DC,∴DE∥AB1
又AB1 平面DBC1,DE
平面DBC1,DE 平面DBC1
平面DBC1
∴AB1∥平面DBC1
(2)解:作DF⊥BC,垂足为F,因为面ABC⊥面B1BC1,所以DF⊥B1BCC1,连结B1E,则B1E是A1B在平面B1BCC1内的射影
∵BC1⊥AB1 ∴BC1⊥B1E
∵B1BCC1是矩形
∴∠B1BF=BC1C=90°
∴ΔB1BF∽ΔBCC1
∴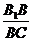 =
= =
=
又F为正三角形ABC的BC边中点
因而B1B2=BF·BC=2
于是B1F2=B1B2+BF2=3,∴B1F=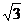
即线段AB1在平面B1BCC1内的射影长为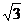
457.求证:底面是梯形的直棱柱的体积,等于两个平行侧面面积的和与这两个侧面间距离的积的一半.
已知:直四棱柱A1C,如图,它的底面AC为梯形.DC∥AB,侧面A1B与侧面D1C的距离为h.
求证: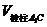 =
= (
(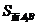 +
+ )×h
)×h

证:设D1E1是梯形A1B1C1D1的高,
∵D1E1⊥A1B1,D1E1 面A1C1
面A1C1
面A1C1⊥面A1B,面A1C1∩面A1B=A1B1.
∴D1E1⊥面A1B.
∴D1E1=h.
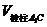 =S底·AA1
=S底·AA1
= (D1C1+A1B1)·D1E1·AA1
(D1C1+A1B1)·D1E1·AA1
= (D1C1·A1A+A1B1·A1A)·h
(D1C1·A1A+A1B1·A1A)·h
= (
( +
+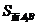 )·h
)·h
456.求证:(1)平行六面体的各对角线交于一点,并且在这一点互相平分.
(2)对角线相等的平行六面体是长方体.
已知:平行六面体ABCD-A1B1C1D1
求证:(1)对角线AC1、BD1、CA1、DB1相交于一点,且在这点互相平分;
(2)若AC1=BD1=CA1=DB1时,该平行六面体为长方体.
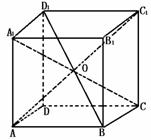
证明:(1)∵AA1∥BB1,BB1∥CC1,
∴AA1∥CC1.
∴对面角A1ACC1是平行四边形.
∴CA1与AC1相交,且互相平分.
设CA1∩AC1=0,则O为CA1,AC1的中点.
同理,可证DB1与AC1及AC1与D1B也相交于一点,且互相平分.
交点也是O.
∴AC1、BD1、DB1、CA1交于一点,且互相平分.
(2)∵平行六面体AC1的对角线面A1C1CA、B1D1DB都是平行四边形.且它们的对角线A1C、B1D、C1A、D1B都相等.
∴对角面A1C1AC,B1D1DB都是矩形.
因此 CC1⊥A1C1
∴BB1⊥B1D1
又∵BB1∥CC1
∴BB1⊥A1C1
∴BB1⊥平面A1C1
∴平行六面体A1C是直平行六面体
同理可证:CB⊥平面A1B,则BC⊥AB.
∴平面四边形ABCD是矩形.
∴直平行六面体A1C是长方体.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com