525.　 如图，四面体ABCD的棱BD长为2，其余各棱的长均是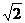，求：二面角A-BD-C、A-BC-D、B-AC-D的大小.

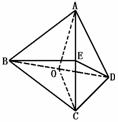
解析：(1)取BD的中点O，连AO、OC.

在ΔABD中，∵AB＝AD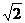＝，BD＝2，

∴ΔABD是等腰直角三角形，AO⊥BD，同理OC⊥BD.

∴∠AOC是二面角A-BD-C的平面角

又AO＝OC＝1，AC＝，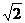

∴∠AOC＝90°.

即二面角A-BD-C为直二面角.

(2)∵二面角A-BD-C是直二面角，AO⊥BD，∴AO⊥平面BCD.

∴ΔABC在平面BCD内的射影是ΔBOC.

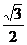∵S_ΔOCB＝,S_ΔABC＝,∴cosθ＝.

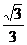即二面角A-BC-D的大小是arccos.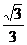

(3)取AC的中点E，连BE、DE.

∵AB＝BC，AD＝DC，

∴BD⊥AC，DE⊥AC，∴∠BED就是二面角的平面角.

在ΔBDE中，BE＝DE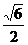＝，由余弦定理，得cosα＝-

∴二面角B-AC-D的大小是π-arccos.

评析　 本例提供了求二面角大小的方法：先作出二面角的平面角，再利用其所在的三角形算出角的三角函数值，或利用面积的射影公式S′＝S·cosθ求得.

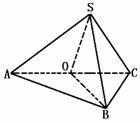
524.　 在三棱锥S-ABC中，∠ASB＝∠BSC＝60°，∠ASC＝90°，且SA＝SB＝SC，求证：平面ASC⊥平面ABC.

证明　 取AC的中点O，连SO、BO，由已知，得ΔSAB、ΔSBC都是正三角形.∴BC＝AB＝a,SA＝SC＝a,又SO⊥AC，BO⊥AC，∴∠SOB就是二面角S-AC-B的平面角.又∵SA＝AB＝a,SC＝BC＝a,AC＝AC,∴ΔACS≌ΔACB.

∴SO＝BO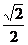＝a.

在ΔSOB中，∵SB＝a,∴∠SOB＝90°.

即平面SAC⊥平面ABC.

另证：过S作SO⊥平面ABC，垂足是O.∵SA＝SB＝SC，∴S在平面内的射影是ΔABC的外心，同前面的证明，可知ΔABC是直角三角形，∴O在斜边AC上.

又∵平面SAC经过SO，∴平面SAC⊥平面ABC

说明　 证明“面面垂直”的常用方法是根据定义证明平面角是90°，或利用判定定理证明一个平面经过另一个平面的垂线.

523. 直线a、b是异面直线，a⊥平面α，b⊥平面β，a⊥b，求证：α⊥β.

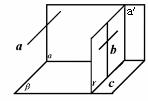
证明　 过b上任意一点作直线a′，使a∥a′.∵a⊥b,∴a′⊥b.

设相交直线a′、b确定一个平面,∩β＝c.∵b⊥β,cβ,∴b⊥c.

在平面内，b⊥c,b⊥a′,∴a′∥c.∴a∥a′∥c.又∵a⊥α,∴c⊥α,cβ，∴β⊥α

522. 已知正四棱锥的各条棱都是a.

(1)求底面一边到相对侧面的距离；

(2)求证：相邻两侧面所成二面角等于侧面和底面所成二面角的2倍；

(3)求相对两侧面所成二面角的余弦值.

(1)解：　 作PO⊥底面ABCD，垂足是O，取BC、AD、PB的中点F、E、M，连结PE、PF、EF、OM、MC、MA.

∵AD∥BC，∴AD∥平面PBC，AD到平面PBC的距离就是E点到平面PBC的距离，∵BC⊥平面PEF，∴平面PEF⊥平面PBC.∴E点到交线PF的距离就是E点到平面PBC的距离d.

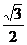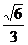∴d·PF＝PO·EF,d·a＝a·,∴d＝a.

(2)在ΔACM中，∵AM＝MC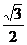＝a,AD＝OC,∴OM是∠AMC的平分线，又AM⊥PB，CM⊥PB，∴∠AMC是二面角A-PB-C的平面角，∠OFP是二面角P-BC-AD的平面角.

又∵AO＝PO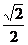＝a,AM＝PF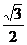＝a,∴RtΔPOF≌RtΔAMO.

∴∠AMC＝2∠PFO，∴命题成立.

(3)设相对两侧面PBC、PAD的交线是l，∵AD∥BC，∴AD∥平面PBC，∴AD∥l，∵BC⊥平面PEF，∴l⊥平面PEF，∴∠EPF就是所求二面角的平面角.

∴cos∠EPF＝＝.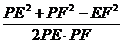

521. 　已知边长为10的正ΔABC的顶点A在平面α内，顶点B、C在平面α同侧，BD为AC边上的中线，B、C到平面α的距离分别是BB₁＝2，CC₁＝4

(1)求证：BB₁∥平面ACC₁

(2)求证：BD⊥平面ACC₁

(3)求四棱锥A-BCC₁B₁的体积

解析： 本小题考查空间图形线、面的平行、垂直关系，考查逻辑思维能力和运算能力.

解　 (1)∵BB₁⊥α，CC₁⊥α，∴BB₁∥CC₁

∵BB₁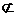平面ACC₁，CC₁平面ACC₁，

∴BB₁∥平面ACC₁.

(2)∵

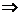
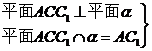
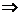过D点作AC₁的垂线DD₁，则DD₁⊥α.

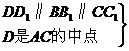
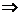∵DD₁＝CC₁＝×4＝2＝BB₁，

∴四边形B₁BDD₁是矩形

∴B₁D₁∥BD

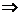
∵BD⊥平面ACC₁

(3)在RtΔABD中，BD＝＝＝B₁D₁

在RtΔACC₁中，AC₁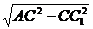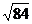＝＝，连结BC₁，

则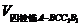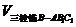＝+＝××AC₁×B₁D₁×BB₁+××AC₁×CC₁×BD.

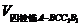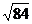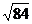∴＝××××2+××××4＝30.

520.　 如图，在正三棱柱ABC-A₁B₁C₁中E∈BB₁，截面A₁EC⊥侧面AC₁

(1)求证：BE＝EB₁

(2)若AA₁＝A₁B₁，求平面A₁EC与平面A₁B₁C₁所成二面角(锐角)的度数

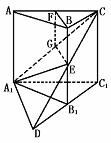
解析： 欲证BE＝EB₁，可证A₁E＝EC，由截面A₁EC⊥侧面AC₁，考虑到作EG⊥A₁C于G，关键在于证出G是A₁C的中点，为了利用正棱柱的性质，可取AC中点F，证FG∥AA₁即可.

证明：　 (1)在截面A₁EC中，作EG⊥A₁C于G，∵面A₁EC⊥面A₁C，∴EG⊥面A₁C，取AC中点F，连BF、FG，易证EBFG为平行四边形，∴BE＝FG，又证得FG＝AA₁，∴BE＝AA₁＝BB₁，即BE＝EB₁.

(2)分别延长CE、C₁B₁交于点D，连A₁D，利用E是BB₁的中点，可证得A₁C₁⊥A₁D，由三垂线定理，可证出A₁C⊥A₁D，

∴∠CA₁C₁为所求二面角的平面角，由A₁A＝A₁C，得∠CA₁C₁＝45°.

评析　 本题解题思路：由证E是BB₁的中点证G是A₁C的中点GF∥AA₁，要完成此过程，除具有扎实的立几基本功外，尚需很好的平几修养，确实是一个考查基础知识很全面的好题.

519.三棱锥的三个侧面互相垂直，它们的面积分别为6m²,4m²和3m²，求它的体积.

解析：设三棱锥S-ABC的三条侧棱长分别为xm,ym,zm.则三个侧面积分别为、、.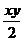

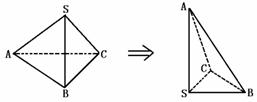
依题意： 则　 xyz＝24

而　 V_S-ABC＝V_A-SBC＝·yz·x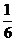＝×24＝4(m³)

∴它的体积为4m³.

518.将正方体截去一个角，求证：截面是锐角三角形.

已知：正方体中截去以P为顶点的一角得截面ABC.

求证：ΔABC是锐角三角形.

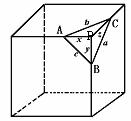
证明：如图，P-ABC是一个四面体.

∵ΔPAB、ΔPBC、ΔPCA都是直角三角形.

∴ 则　 z²＝(a²+b²-c²)

∵z≠0，∴a²+b²-c²＞0

即　 c²＜a²+b²,∴b²＜a²+c².

∴∠BAC、∠ABC都小于90°.

∴ΔABC为锐角三角形.

517.　 如图三棱锥P-ABC中，PA＝a,AB＝AC＝2a,∠PAB＝∠PAC＝∠BAC＝60°，求三棱锥P-ABC的体积.

解法一：过点P作PO⊥平面ABC于点O，∵∠PAB＝∠PAC＝∠BAC＝60°

∴AO平分∠BAC

∴cos∠PAO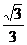＝＝，∴sin∠PAO＝＝

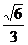
∴PO＝asin∠PAO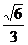＝a

∴V_棱锥＝××2a×2asin60°×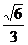a＝a³

点评　 这种方法叫直接法，就是利用锥体的体积公式直接计算，这是一种常规方法，必须掌握.

解法二：取AB、AC中点M、N的连结PM、PN

∵PA＝a,AB＝AC＝2a,∠PAB＝∠PAC＝∠BAC＝60°

∴三棱锥P-AMN为棱长为a的正四面体，且S_ΔAMN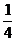＝S_ΔABC

∴V_P-AMN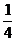＝V_P-ABC，而V_P-AMN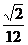＝a³

∴V_P-ABC＝4V_P-AMN＝a³

点评 　此法是根据棱长与含有60°角的三角形的关系，把锥体截成棱长相等的三棱锥，然后根据小锥体的体积与原棱锥的体积关系，求原棱锥的体积.

解法三　 在ΔPAB中，PA＝a,AB＝2a

又∠PAB＝60°，∴∠APB＝90°

同理∠APC＝90°∴AP⊥平面PBC

又S_ΔPBC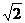＝a² ∴V_P-ABC＝V_A-PBC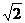＝·a²·a＝a³.

516. 　在三棱锥A-BCD中，ΔABC和ΔBCD都是边长为a的正三角形，二面角A-BC-D＝φ，问φ为何值时，三棱锥的全面积最大。

解析：S_ΔBAC＝S_ΔBCD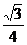＝a²为常量，所以三棱锥全面积的大小取决于S_ΔABD与S_ΔACD的大小，由于ΔABD≌ΔACD，所以只求S_ΔACD何时面积取最大值即可。∵S_ΔACD＝asin∠ACD，所以当∠ACD＝90°时面积最大，问题得解。

解　 如图，取BC中点M，连AM、DM，∴ΔABC和ΔBCD都是正三角形，∴∠AMD是二面角A-BC-D的平面角，∠AMD＝φ，又∵ΔABD≌ΔACD，且当∠ACD＝90°时，ΔACD和ΔABD面积最大，此时AD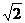＝a，在ΔAMD中，由余弦定理cos∠AMD＝-，

∴当φ＝π-arccos时，三棱锥A-BCD的全面积最大。

点评　 本题将求棱锥全面积的最大值，转化为求ΔACD面积的最大值，间接求得φ角。