
3. [2009届广东省六校第二次联考高三年级文科数学试卷第7题]
已知等差数列 中,
中,  是方程
是方程 的两根, 则
的两根, 则 等于( )
等于( )
A.  B.
B.  C.
C.  D.
D.
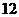
2.[山东省泰安英雄山中学2009届高三年级测试数学文科卷第5题]
等差数列 各项都是负数,且
各项都是负数,且 ,则它的前10项和S10等于( )
,则它的前10项和S10等于( )
A.-15 B.-13 C.-11 D.-9
1. [广东省实验中学2008学年高三第二次阶段测试试卷数学(文科)第7题]
已知数列{an}为等差数列,Sn为其前n项和,且a6-a4= 4, a11=21, Sk= 9则k的值为( )
A.2 B. 3 C.4 D.5
28.(江安中学)已知两点F1(-3,0)、F2(3,0),且点P使 ,又向量
,又向量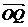 是单位向量。①求点
是单位向量。①求点 的轨迹;
的轨迹;
②若点Q的坐标为 ,求数量积
,求数量积 的取值范围。
的取值范围。
正解:求出 ,依题
,依题 ,
, 是
是 的两根,判断出
的两根,判断出 ,及
,及 时所取的极值是极大值还是极小值,再由
时所取的极值是极大值还是极小值,再由 ,求出
,求出 及极大值和极小值。
及极大值和极小值。
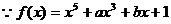


 时有极值
时有极值 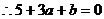
 代入
代入 得
得


 仅当
仅当 时有极值,
时有极值,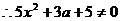 对任意
对任意 成立
成立


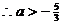 ,考察
,考察 ,
, 随
随 的变化表。
的变化表。
27.(江安中学)在 中,
中, ,
, D是线段AB的垂直平分线上的一点,D到AB的距离为2,过C的曲线E上任一点P满足
D是线段AB的垂直平分线上的一点,D到AB的距离为2,过C的曲线E上任一点P满足 为常数。
为常数。
4) 建立适当的坐标系,并求出曲线E的方程。
5)
过点D的直线 与曲线E相交于不同的两点M,N,且M点在D,N之间,若
与曲线E相交于不同的两点M,N,且M点在D,N之间,若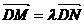 ,求
,求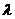 的取值范围。
的取值范围。
正解:①以 所在直线分别为X轴,Y轴建立直角坐标系
所在直线分别为X轴,Y轴建立直角坐标系
 =
= =
= ,
,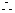 动点的轨迹方程为以
动点的轨迹方程为以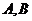 为焦点的椭圆
为焦点的椭圆

② 与
与 轴重合,
轴重合,
 与
与 轴不重合,
轴不重合, 令直线
令直线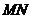 的方程为:
的方程为: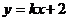 与曲线
与曲线 的方程联立得
的方程联立得
 ,
,
 ,∴
,∴ ,
,

∴ ,∴
,∴ ,∵
,∵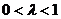 ,∴
,∴ ,综上
,综上 ≤
≤
误解:由 的范围求
的范围求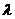 的范围时注意方法,方法不对,可能就会导致错误结果。
的范围时注意方法,方法不对,可能就会导致错误结果。
26. (江安中学)如图,已知一次函数
(江安中学)如图,已知一次函数 与二次函数
与二次函数 的图像相交于
的图像相交于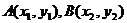 两点,其中
两点,其中 ,且
,且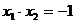 ,点F(0,b),
,点F(0,b),
1)
求 的值
的值
2)
求t关于 的函数关系式
的函数关系式
3)
当 时,求以原点为中心,F为一个焦点,且过点B的椭圆方程
时,求以原点为中心,F为一个焦点,且过点B的椭圆方程
正解:①由



 =
=
 =
=
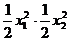 =
=
②
 ,
,
而 是方程
是方程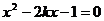 的根,
的根,
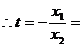
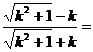

③
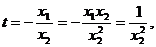

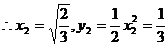 ,得
,得
 为焦点,故半焦距为
为焦点,故半焦距为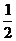 。
。
设椭圆方程为 ,将B点坐标代入方程,解得
,将B点坐标代入方程,解得 (
(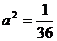 舍去)
舍去)
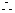 所求椭圆方程为
所求椭圆方程为
误解:①中公式要记清:
②中计算导致错误
25.(蒲中)过点A(1,1)作直线l与双曲线 =1交于P1、P2两个不同点,若A为P1P2中点,求直线l的方程。
=1交于P1、P2两个不同点,若A为P1P2中点,求直线l的方程。
解:设P1(x1,y1),P2(x2,y2),则2x12-y12=2,2x22-y22=2
两式相减得2(x1+x2)(x1-x2)-(y1+y2)(y1-y2)=0,
当x1≠x2时,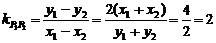
∴直线l的方程 2x-y-1=0 将y=2x-1代入 得
得
2x2-4x+3=0 方程无解 ∴直线不存在
当x1=x2时,直线方程为x=1,与双曲线仅有一个公共点。综上所述,直线l不存在。
点评:本题易错点一是用“差分法”求出斜率后就给出结论而不去验证导致错误;二是忽视x1=x2时情况的讨论。
24.(薛中)已知定点A(3,0),B(0,3)如果线段AB与抛物线 有且仅有一个公共点,试求m的取值范围。
有且仅有一个公共点,试求m的取值范围。


 答案:设线段AB上任意一点
答案:设线段AB上任意一点 ,可看作线段AB的定比分点,所以
,可看作线段AB的定比分点,所以 
 ,由线段AB与抛物线C有且仅有一个公共点,所以方程
,由线段AB与抛物线C有且仅有一个公共点,所以方程 有且仅有一个正根,所以
有且仅有一个正根,所以  1或
1或  2
2
解1得m=3, 解2得m> ,综上所述m>
,综上所述m> 或m=3。
或m=3。
错解:直线AB的方程为y=-x+3,因为AB与抛物线C有且仅有一个公共点,所以方程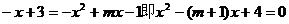 的判别
的判别
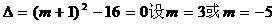 。
。
错因:审题不严,显现条件弱用,把求线段AB与抛物线C的交点变成了求直线AB与抛物线C的交点。
23.(薛中)直线 与双曲线
与双曲线 相交于点A,B,是否存在这样的实数a,使得A,B关于直线
相交于点A,B,是否存在这样的实数a,使得A,B关于直线 对称?如果存在,求出实数a,如果不存在,请说明理由。
对称?如果存在,求出实数a,如果不存在,请说明理由。
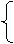 答案:设存在实数a,使得A,B关于y=2x对称,又设
答案:设存在实数a,使得A,B关于y=2x对称,又设 ,
, ,则
,则 而
而 由
由  作差整理可得:
作差整理可得:
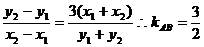 由
由 ,故不存在这样的实数a。
,故不存在这样的实数a。
错解: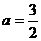
错因:没有挖掘隐含条件,而轴对称的第二个条件直线AB与直线 垂直,造成解题错误。
垂直,造成解题错误。
22.(薛中)设椭圆方程为 ,试求满足下列条件的圆方程:1圆心在椭圆的长轴上;2与椭圆的短轴相切;3与椭圆在某点处也相切。
,试求满足下列条件的圆方程:1圆心在椭圆的长轴上;2与椭圆的短轴相切;3与椭圆在某点处也相切。
答案:根据题意设圆方程为 1,化椭圆方程为
1,化椭圆方程为 2,由12消去y,得:
2,由12消去y,得: ,由圆与椭圆相切:
,由圆与椭圆相切: 即所求圆的方程为:
即所求圆的方程为: ,另由图可知
,另由图可知 也合题意。
也合题意。
错解:
错因:漏解
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com