
2. (1)
∵A,B两点的坐标分别是A(10,0)和B(8, ),
),
∴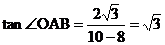 ,
,
∴
当点A´在线段AB上时,∵ ,TA=TA´,
,TA=TA´,
∴△A´TA是等边三角形,且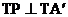 ,
,
∴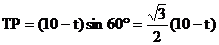 ,
,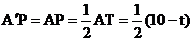 ,
,
|
|
|
 ∴
∴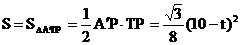 ,
,
|
|
|
|
|
|
|
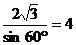 ,
,
所以此时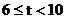 .
.
(2)当点A´在线段AB的延长线,且点P在线段AB(不与B重合)上时,
纸片重叠部分的图形是四边形(如图(1),其中E是TA´与CB的交点),
|
|
|
 当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
又由(1)中求得当A´与B重合时,T的坐标是(6,0)
|
|
|
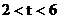 .
.
|
|
|
|
|
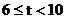 时,
时,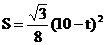 ,
,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是 .
.
2当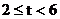 时,由图1,重叠部分的面积
时,由图1,重叠部分的面积
∵△A´EB的高是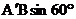 ,
,
∴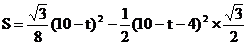
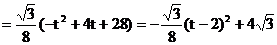
当t=2时,S的值最大是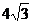 ;
;
3当 ,即当点A´和点P都在线段AB的延长线是(如图2,其中E是TA´与CB的交点,F是TP与CB的交点),
,即当点A´和点P都在线段AB的延长线是(如图2,其中E是TA´与CB的交点,F是TP与CB的交点),
∵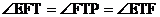 ,四边形ETAB是等腰形,∴EF=ET=AB=4,
,四边形ETAB是等腰形,∴EF=ET=AB=4,
∴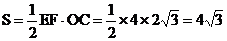
综上所述,S的最大值是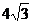 ,此时t的值是
,此时t的值是 .
.
1.
解:( 1)由已知得:
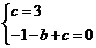 解得
解得
c=3,b=2
 ∴抛物线的线的解析式为
∴抛物线的线的解析式为
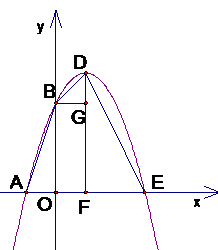
(2)由顶点坐标公式得顶点坐标为(1,4)
所以对称轴为x=1,A,E关于x=1对称,所以E(3,0)
设对称轴与x轴的交点为F
所以四边形ABDE的面积=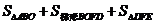
=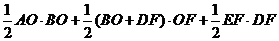
=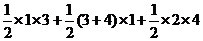
=9
(3)相似
如图,BD=
BE=
DE=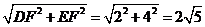
所以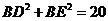 ,
,  即:
即: 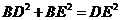 ,所以
,所以 是直角三角形
是直角三角形
所以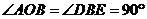 ,且
,且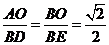 ,
,
所以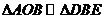 .
.
29. (2008年江苏省无锡市)一种电讯信号转发装置的发射直径为31km.现要求:在一边长为30km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:
(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?
(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?
答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km的正方形城区示意图,供解题时选用)
|
|
|
|
压轴题答案
28. (2008年江苏省南通市)已知双曲线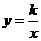 与直线
与直线 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线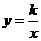 上的动点.过点B作BD∥y轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴于点D.过N(0,-n)作NC∥x轴交双曲线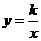 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
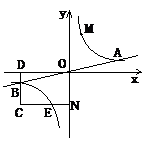
27. (2008年山东省青岛市)已知:如图①,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
(1)当t为何值时,PQ∥BC?
(2)设△AQP的面积为y(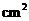 ),求y与t之间的函数关系式;
),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.


26. (2008年陕西省)某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站.由供水站直接铺设管道到另外两处.
如图,甲,乙两村坐落在夹角为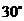 的两条公路的
的两条公路的 段和
段和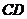 段(村子和公路的宽均不计),点
段(村子和公路的宽均不计),点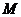 表示这所中学.点
表示这所中学.点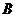 在点
在点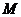 的北偏西
的北偏西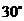 的3km处,点
的3km处,点 在点
在点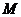 的正西方向,点
的正西方向,点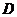 在点
在点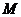 的南偏西
的南偏西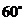 的
的 km处.
km处.
为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:
方案一:供水站建在点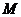 处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
方案二:供水站建在乙村(线段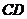 某处),甲村要求管道建设到
某处),甲村要求管道建设到 处,请你在图①中,画出铺设到点
处,请你在图①中,画出铺设到点 和点
和点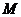 处的管道长度之和最小的线路图,并求其最小值;
处的管道长度之和最小的线路图,并求其最小值;
方案三:供水站建在甲村(线段 某处),请你在图②中,画出铺设到乙村某处和点
某处),请你在图②中,画出铺设到乙村某处和点 处的管道长度之和最小的线路图,并求其最小值.
处的管道长度之和最小的线路图,并求其最小值.
综上,你认为把供水站建在何处,所需铺设的管道最短?


25. (2008年上海市)已知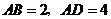 ,
,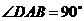 ,
,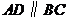 (如图13).
(如图13).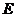 是射线
是射线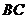 上的动点(点
上的动点(点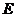 与点
与点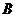 不重合),
不重合),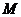 是线段
是线段 的中点.
的中点.
(1)设 ,
,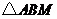 的面积为
的面积为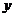 ,求
,求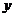 关于
关于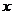 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(2)如果以线段 为直径的圆与以线段
为直径的圆与以线段 为直径的圆外切,求线段
为直径的圆外切,求线段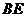 的长;
的长;
(3)联结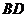 ,交线段
,交线段 于点
于点 ,如果以
,如果以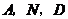 为顶点的三角形与
为顶点的三角形与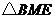 相似,求线段
相似,求线段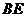 的长.
的长.

24.(2008年大庆市)
如图①,四边形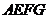 和
和 都是正方形,它们的边长分别为
都是正方形,它们的边长分别为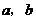 (
(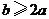 ),且点
),且点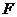 在
在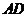 上(以下问题的结果均可用
上(以下问题的结果均可用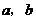 的代数式表示).
的代数式表示).
(1)求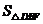 ;
;
(2)把正方形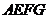 绕点
绕点 按逆时针方向旋转45°得图②,求图②中的
按逆时针方向旋转45°得图②,求图②中的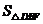 ;
;
(3)把正方形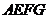 绕点
绕点 旋转一周,在旋转的过程中,
旋转一周,在旋转的过程中,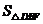 是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.
是否存在最大值、最小值?如果存在,直接写出最大值、最小值;如果不存在,请说明理由.
.
23.(天津市2008年)已知抛物线 ,
,
(Ⅰ)若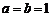 ,
,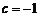 ,求该抛物线与
,求该抛物线与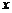 轴公共点的坐标;
轴公共点的坐标;
(Ⅱ)若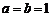 ,且当
,且当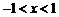 时,抛物线与
时,抛物线与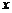 轴有且只有一个公共点,求
轴有且只有一个公共点,求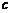 的取值范围;
的取值范围;
(Ⅲ)若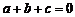 ,且
,且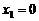 时,对应的
时,对应的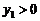 ;
;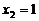 时,对应的
时,对应的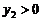 ,试判断当
,试判断当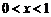 时,抛物线与
时,抛物线与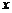 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
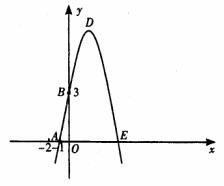
22.(2008年四川省宜宾市)已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
(1)求该抛物线的解析式;
(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
(注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为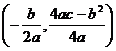 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com