
2.(2005年北京春)“ab<0”是“曲线ax2+by2=1为双曲线”的
(A)充分不必要条件 (B)必要不充分条件 (C)充分必要条件 (D)既不充分又不必要条件
1.设P是双曲线 -
-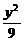 =1上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线的左、右焦点.若|PF1|=3,则|PF2|等于( )
=1上一点,双曲线的一条渐近线方程为3x-2y=0,F1、F2分别是双曲线的左、右焦点.若|PF1|=3,则|PF2|等于( )
(A)1或5 (B)6 (C)7 (D)9
5.给定了双曲线方程,就可求得确定的两条渐近线.但已知渐近线方程,只是限制了双曲线张口的大小,不能直接写出双曲线方程.但若已知渐近线方程是 ±
±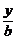 =0,则可把双曲线方程表示为
=0,则可把双曲线方程表示为 -
- =
= (
( ≠0),再根据已知条件确定
≠0),再根据已知条件确定 的值,求出双曲线的方程.
的值,求出双曲线的方程.
[基础闯关]
4.在运用双曲线的第二定义时,一定要注意是动点P到焦点的距离与到相应准线距离之比为常数e.若使用的焦点与准线不是对应的,则上述之比就不再是常数了.
3.参数a、b是双曲线的定形条件,两种标准方程中,总有a>0,b>0;双曲线焦点位置决定标准方程的类型;a、b、c的关系是c2=a2+b2;在方程Ax2+By2=C中,只要AB<0且C≠0,就是双曲线的方程.
2.双曲线的定义用代数式表示为||MF1|-|MF2||=2a,其中2a<|F1F2|,这里要注意两点:
(1)距离之差的绝对值.
(2)2a<|F1F2|,这两点与椭圆的定义有本质的不同.
当|MF1|-|MF2|=2a时,曲线仅表示焦点F2所对应的一支;
当|MF1|-|MF2|=-2a时,曲线仅表示焦点F1所对应的一支;
当2a=|F1F2|时,轨迹是一直线上以F1、F2为端点向外的两条射线;
当2a>|F1F2|时,动点轨迹不存在.
|
方程 |
 |
 |
|
图 形 |
 |
 |
|
范围 |
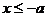 或 或 |
|
|
对称性 |
关于 轴, 轴, 轴及原点对称 轴及原点对称 |
关于 轴, 轴, 轴及原点对称 轴及原点对称 |
|
顶点 |
|
 |
|
离心率 |
|
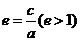 |
|
准线 |
 |
|
|
渐近线 |
|
 |
[特别提醒]
本节的重点是双曲线的定义、方程、几何性质.难点是理解参数a、b、c、e的关系及渐近线方程、准线方程、第二定义的应用.关键是准确理解和掌握有关概念,灵活地运用数形结合、函数与方程的思想及等价转化的思想.为此建议在复习中注意以下几点:
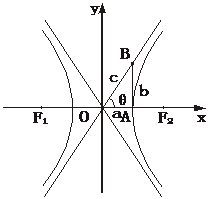
1.双曲线中有一个重要的Rt△OAB(如下图),它的三边长分别是a、b、c.易见c2=a2+b2,若记∠AOB=θ,则e= =
= .
.
3.当双曲线的焦点在 轴上时,双曲线的标准方程为 ,其中焦点坐标为
轴上时,双曲线的标准方程为 ,其中焦点坐标为 ,
, ,且
,且 ;
;
当双曲线的焦点在 轴上时,双曲线的标准方程为 ,其中焦点坐标为
轴上时,双曲线的标准方程为 ,其中焦点坐标为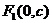 ,
,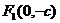 ,且
,且 .
.
当且仅当双曲线的中心在坐标原点,其焦点在坐标轴上时,双曲线的方程才是标准形式。
2.双曲线的第二定义:平面内,到定点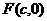 (或
(或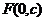 )的距离与到定直线
)的距离与到定直线 的距离之比是常数
的距离之比是常数 (即 )的动点的轨迹叫做双曲线,这个定点是双曲线的 ,这条定直线叫做双曲线的
,其中常数
(即 )的动点的轨迹叫做双曲线,这个定点是双曲线的 ,这条定直线叫做双曲线的
,其中常数 叫做双曲线的 。
叫做双曲线的 。
1.双曲线的定义:我们把平面内与两个定点 的距离的差的绝对值等于常数(
的距离的差的绝对值等于常数( 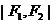 )的点的轨迹叫做双曲线,用符号表示为 。这两个定点叫双曲线的 ,两个焦点之间的距离叫做双曲线的 。
)的点的轨迹叫做双曲线,用符号表示为 。这两个定点叫双曲线的 ,两个焦点之间的距离叫做双曲线的 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com