
6.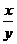 >1的一个充分不必要条件是 ( )
>1的一个充分不必要条件是 ( )
A.x>y B.x>y>0 C.x<y D.y<x<0
5.已知全集U=R,A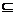 U,如果命题p:
U,如果命题p: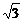 ∈A∪B,则命题“非p”是 ( )
∈A∪B,则命题“非p”是 ( )
A.非p: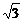
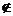 A B.非p:
A B.非p: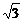 ∈CUB
∈CUB
C.非p: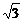
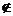 A∩B D.非p:
A∩B D.非p: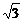 ∈(CUA)∩(CUB)
∈(CUA)∩(CUB)
4.对于直角坐标平面内的任意两点A(x ,
, y
y )、B(x
)、B(x ,y
,y ),定义它们之间的一种“距离”:
),定义它们之间的一种“距离”:
‖AB‖=︱x -x
-x ︱+︱y
︱+︱y -y
-y ︱。给出下列三个命题:
︱。给出下列三个命题:
①若点C在线段AB上,则‖AC‖+‖CB‖=‖AB‖;
②在△ABC中,若∠C=90°,则‖AC‖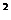 +‖CB‖
+‖CB‖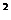 =‖AB‖
=‖AB‖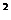 ;
;
③在△ABC中,‖AC‖+‖CB‖>‖AB‖.
其中真命题的个数为 ( )
A.1个 B.2个 C.3个 D.4个
3.下面说法正确的有 ( )
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关;
A.1个 B.2个 C.3个 D.4个
2.关于x的方程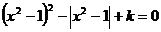 ,给出下列四个命题:
,给出下列四个命题:
①存在实数 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数 ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是 ( )
A.0 B.1 C.2 D.3
1.下列说法正确的是 ( )
A.由合情推理得出的结论一定是正确的.B.合情推理必须有前提有结论.
C.合情推理不能猜想. D.合情推理得出的结论无法判定正误
22.(14分)在线段AD上任取两点B、C,在B、C处折断此线段而得一折线,求此折线能构成三角形的概率.
21.(12分)(理)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为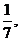 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中所有的白球的个数;
(II)求随机变量 的概率分布;
的概率分布;
(III)求甲取到白球的概率.
(文)每次抛掷一枚骰子(六个面上分别标以数字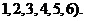
(I)连续抛掷2次,求向上的数不同的概率;
(II)连续抛掷2次,求向上的数之和为6的概率;
(III)连续抛掷5次,求向上的数为奇数恰好出现3次的概率。
20.(12分)设人的某一特征(如眼睛大小)是由他的一对基因决定的,以d表示显性基因,r表示隐性基因,则具有dd基因的人为纯显性,具有rr基因的人为纯隐性,具有rd基因的人为混合性,孩子从父母身上各得一个基因,假定父母都是混合性,求:(1)孩子为纯显性的概率;(2)孩子为纯隐性的概率;(3)孩子为混合性的概率.
19.(12分)(理)在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布 。已知成绩在90分以上(含90分)的学生有12名。
。已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)试问此次参赛学生总数约为多少人?
(Ⅱ)若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?可共查阅的(部分)标准正态分布表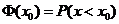
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1.2 1.3 1.4 1.9 2.0 2.1 |
0.8849 0.9032 0.9192 0.9713 0.9772 0.9821 |
0.8869 0.9049 0.9207 0.9719 0.9778 0.9826 |
0.888 0.9066 0.9222 0.9726 0.9783 0.9830 |
0.8907 0.9082 0.9236 0.9732 0.9788 0.9834 |
0.8925 0.9099 0.9251 0.9738 0.9793 0.9838 |
0.8944 0.9115 0.9265 0.9744 0.9798 0.9842 |
0.8962 0.9131 0.9278 0.9750 0.9803 0.9846 |
0.8980 0.9147 0.9292 0.9756 0.9808 0.9850 |
0.8997 0.9162 0.9306 0.9762 0.9812 0.9854 |
0.9015 0.9177 0.9319 0.9767 0.9817 0.9857 |
(文)某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营业区内的电话通话时间情况,其原始数据如下表所示:
|
|
A |
B |
C |
D |
E |
|
第一次通话时间 |
3分 |
3分45秒 |
3分55秒 |
3分20秒 |
6分 |
|
第二次通话时间 |
0分 |
4分 |
3分40秒 |
4分50秒 |
0分 |
|
第三次通话时间 |
0分 |
0分 |
5分 |
2分 |
0分 |
|
应缴话费(元) |
|
|
|
|
|
(1)在上表中填写出各人应缴的话费;
(2)设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况统计表):
|
时间段 |
频数累计 |
频数 |
频率 |
累计频率 |
|
0<t≤3 |
┯ |
2 |
0.2 |
0.2 |
|
3<t≤4 |
|
|
|
|
|
4<t≤5 |
|
|
|
|
|
5<t≤6 |
|
|
|
|
|
合计 |
正 正 |
|
|
|
(3)若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算)。问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com