
6.已知平面上直线l的方向向量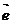 =
=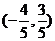 ,点O(0,0)和A(1,-2)在l上的射影分别是O1和A1,若
,点O(0,0)和A(1,-2)在l上的射影分别是O1和A1,若
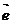 ,则λ= ( )
,则λ= ( )
A. B.-
B.- C.2 D.-2
C.2 D.-2
5.若 与
与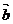 -
-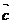 都是非零向量,则“
都是非零向量,则“ ·
·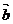 =
= ·
·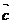 ”是“
”是“ ⊥(
⊥(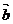 -
-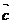 )”的 ( )
)”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.若 、
、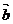 、
、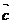 为任意向量,m∈R,则下列等式不一定成立的是 ( )
为任意向量,m∈R,则下列等式不一定成立的是 ( )
A.( +
+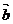 )+
)+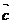 =
= +(
+(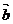 +
+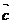 ) B.(
) B.( +
+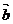 )·
)·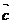 =
= ·
·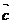 +
+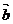 ·
·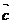
C.m( +
+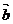 )=m
)=m +m
+m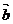 D.(
D.( ·b)
·b)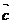 =
= (
(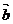 ·
·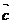 )
)
3.已知 ,
, ,
, ,若
,若 取最小值时,
取最小值时, 的值时( )
的值时( )
A. B.
B.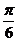 C.
C.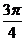 D.
D.
2.(理)已知向量 =(2,4,x),
=(2,4,x),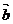 =(2,y,2),若|
=(2,y,2),若| |=6,
|=6, ⊥
⊥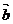 ,则x+y的值是( )
,则x+y的值是( )
A.-3或1 B.3或-1 C.-3 D.1
(文)已知点C在线段AB的延长线上,且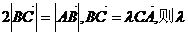 等于 ( )
等于 ( )
A.3 B.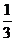 C.
C.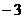 D.
D.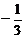
1.(理)下列各组向量共面的是 ( )
A. =(1,2,3),
=(1,2,3),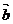 =(3,0,2),
=(3,0,2),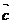 =(4,2,5)
=(4,2,5)
B. =(1,0,0),
=(1,0,0),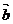 =(0,1,0),
=(0,1,0),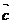 =(0,0,1)
=(0,0,1)
C. =(1,1,0),
=(1,1,0),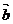 =(1,0,1),
=(1,0,1),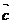 =(0,1,1)
=(0,1,1)
D. =(1,1,1),
=(1,1,1),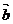 =(1,1,0),
=(1,1,0),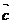 =(1,0,1)
=(1,0,1)
(文)已知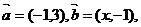 且
且 ∥
∥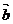 ,则x等于 ( )
,则x等于 ( )
A.3 B.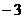 C.
C.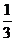 D.
D.
22.证明(1)∵点Pn、Pn+1都在斜率为k的直线上
∴ =k,即
=k,即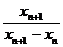 =k,故 (k-1)xn+1=kxn
=k,故 (k-1)xn+1=kxn
∵k≠0,xn+1≠1,xn≠1,
∴ =
= =常数,∴{xn}是公比为
=常数,∴{xn}是公比为 的等比数列。
的等比数列。
(2)答案是肯定的,即存在自然数M,使当n>M时,xn>1恒成立。
事实上,由1<a<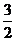 ,得0<2a2-3a+1<1
,得0<2a2-3a+1<1
∵yn=log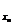 (2a2-3a+1),
(2a2-3a+1),
∴ = log
= log xn
xn
由(1)得{xn}是等比数列,设公比为q>0首项为x1,则xn=x1·qn-1(n∈N)
∴ =(n-1) log
=(n-1) log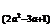 q+log
q+log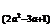 x1
x1
令d=log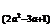 q,故得{
q,故得{ }是以d为公差的等差数列。
}是以d为公差的等差数列。
又∵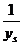 =2t+1,
=2t+1,  =2s+1,∴
=2s+1,∴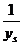 -
- =2(t-s)
=2(t-s)
即(s-1)d-(t-1)d=2(t-s),
∴d=-2
故 =
=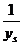 +(n-s)·(-2)=2(t+s)-2n+1,(n∈N)
+(n-s)·(-2)=2(t+s)-2n+1,(n∈N)
又∵xn=(2a2-3a+1)
 (n∈N)
(n∈N)
∴要使xn>1恒成立,即须 <0
<0
∴2(t+s)-2n+1<0,∴n>(t+s)+ ,当M=t+s,n>M时,我们有
,当M=t+s,n>M时,我们有 <0恒成立,
<0恒成立,
∴当n>M=(t+s)时,xn=(2a2-3a+1)
 >1恒成立。(∵0<2a2-3a+1<1)
>1恒成立。(∵0<2a2-3a+1<1)
21.解:(Ⅰ)由已知,得 ,
,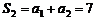 ,
, .
.
由 ,知
,知
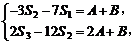 即
即 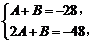
解得 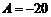 ,
, .
.
(Ⅱ)方法1
由(Ⅰ),得  ,
①
,
①
所以 .
②
.
②
②-①,得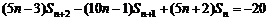 , ③
, ③
所以 . ④
. ④
④-③,得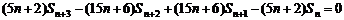 .
.
因为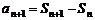 ,
,
所以 .
.
又因为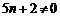 ,
,
所以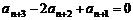 ,
,
即 ,
, .
.
所以数列 为等差数列.
为等差数列.
方法2
由已知,得 ,
,
又 ,且
,且 ,
,
所以数列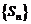 是唯一确定的,因而数列
是唯一确定的,因而数列 是唯一确定的.
是唯一确定的.
设 ,则数列
,则数列 为等差数列,前
为等差数列,前 项和
项和 .
.
于是 ,
,
由唯一性得  ,即数列
,即数列 为等差数列.
为等差数列.
(Ⅲ)由(Ⅱ)可知, .
.
要证 ,
,
只要证 .
.
因为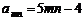 ,
, ,
,
故只要证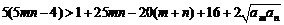 ,
,
即只要证 .
.
因为
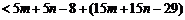
 ,
,
所以命题得证.
20.解:(Ⅰ)依题意有 ,
,
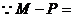
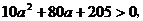
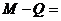
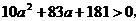
 最大.又
最大.又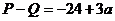 ,
,
当 时,
时,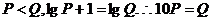 ,
,
满足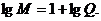
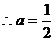 符合题意.
符合题意.
当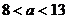 时,
时,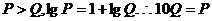 ,
,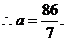
但此时不满足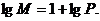
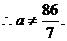
 的前三项为
的前三项为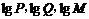 ,此时
,此时 ∴
∴
(Ⅱ)  时,
时,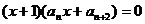
 ,
,
又∵

∴
 =
= .
.
19.解:(1)方法一 用数学归纳法证明:
1°当n=1时,
∴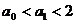 ,命题正确.
,命题正确.
2°假设n=k时有
则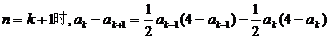

而
又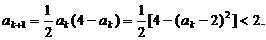
∴ 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有
方法二:用数学归纳法证明:
1°当n=1时,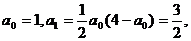 ∴
∴ ;
;
2°假设n=k时有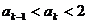 成立,
成立,
令 ,
, 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: 即
即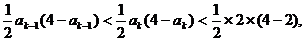
也即当n=k+1时  成立,所以对一切
成立,所以对一切
(2)下面来求数列的通项: 所以
所以
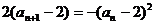
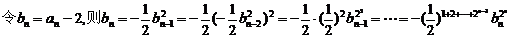 ,
,
又bn=-1,所以
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com