
5.已知集合M={-1,1},N={x| <2x+1<4,x∈Z },则M∩N等于
(
)
<2x+1<4,x∈Z },则M∩N等于
(
)
?A.{-1,1} ?B.{-1} ? C.{0} D.{-1,0}
答案?B?

例1已知a= ,b=9.求:
,b=9.求:
(1)
(2) .
.
解 (1)原式=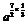 .
. ÷[a
÷[a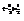 ·
·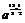 ]
]
= 
 =a
=a .
.
∵a= ,∴原式=3.
,∴原式=3.
(2)方法一 化去负指数后解.
 ∵a=
∵a=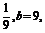 ∴a+b=
∴a+b=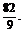
方法二 利用运算性质解.

∵a=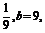 ∴a+b=
∴a+b=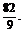
例2 函数f(x)=x2-bx+c满足f(1+x)=f(1-x)且f(0)=3,则f(bx)与f(cx)的大小关系是 ( )
A.f(bx)≤f(cx)? B.f(bx)≥f(cx)
C.f(bx)>f(cx) D.大小关系随x的不同而不同
答案?A
例3 求下列函数的定义域、值域及其单调区间:
(1)f(x)=3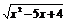 ;
;
(2)g(x)=-(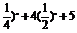 .
.
解 (1)依题意x2-5x+4≥0,
解得x≥4或x≤1,
∴f(x)的定义域是(-∞,1]∪[4,+∞).
令u= ∵x∈(-∞,1]∪[4,+∞),
∵x∈(-∞,1]∪[4,+∞),
∴u≥0,即 ≥0,而f(x)=3
≥0,而f(x)=3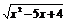 ≥30=1,
≥30=1,
∴函数f(x)的值域是[1,+∞).
∵u= ,∴当x∈(-∞,1]时,u是减函数,
,∴当x∈(-∞,1]时,u是减函数,
当x∈[4,+∞)时,u是增函数.而3>1,∴由复合函数的单调性可知,
f(x)=3 在(-∞,1]上是减函数,在[4,+∞)上是增函数.
在(-∞,1]上是减函数,在[4,+∞)上是增函数.
故f(x)的增区间是[4,+∞),减区间是(-∞,1].
(2)由g(x)=-(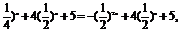
∴函数的定义域为R,令t=( x (t>0),∴g(t)=-t2+4t+5=-(t-2)2+9,
x (t>0),∴g(t)=-t2+4t+5=-(t-2)2+9,
∵t>0,∴g(t)=-(t-2)2+9≤9,等号成立的条件是t=2,
即g(x)≤9,等号成立的条件是( =2,即x=-1,∴g(x)的值域是(-∞,9].
=2,即x=-1,∴g(x)的值域是(-∞,9].
由g(t)=-(t-2)2+9 (t>0),而t=( 是减函数,∴要求g(x)的增区间实际上是求g(t)的减区间,
是减函数,∴要求g(x)的增区间实际上是求g(t)的减区间,
求g(x)的减区间实际上是求g(t)的增区间.
∵g(t)在(0,2]上递增,在[2,+∞)上递减,
由0<t=( ≤2,可得x≥-1, 由t=(
≤2,可得x≥-1, 由t=( ≥2,可得x≤-1.
≥2,可得x≤-1.
∴g(x)在[-1,+∞)上递减,在(-∞,-1]上递增,
故g(x)的单调递增区间是(-∞,-1],单调递减区间是[-1,+∞).
例4 (12分)设a>0,f(x)=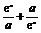 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)求证:f(x)在(0,+∞)上是增函数.
(1)解 ∵f(x)是R上的偶函数,∴f(-x)=f(x),
1分 ∴
∴(a-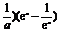 =0对一切x均成立,
3分
=0对一切x均成立,
3分
∴a- =0,而a>0,∴a=1.
4分
=0,而a>0,∴a=1.
4分
(2)证明 在(0,+∞)上任取x1、x2,且x1<x2, 5分
则f(x1)-f(x2)= +
+ -
-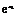 -
-
=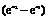 (
(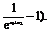 8分
8分
∵x1<x2,∴ 有
有 ?
?
∵x1>0,x2>0,∴x1+x2>0,∴ >1,
10分
>1,
10分
 -1<0.∴f(x1)-f(x2)<0,即f(x1)<f(x2),
-1<0.∴f(x1)-f(x2)<0,即f(x1)<f(x2),
故f(x)在(0,+∞)上是增函数. 12分

4.关于函数f(x)=2x-2-x(x∈R),有下列三个结论:
①f(x)的值域为R;
②f(x)是R上的增函数;
③对任意x∈R,有f(-x)+f(x)=0成立.
其中全部正确的结论是 ( )
?A.①②③ ? B.①③ C.①② D.②③
答案?A?
3. 函数f(x)=ax-b的图象如图所示,其中a、b为常数,则下列结论正确的是
( )?A.a>1,b>0
B.a>1,b<0
函数f(x)=ax-b的图象如图所示,其中a、b为常数,则下列结论正确的是
( )?A.a>1,b>0
B.a>1,b<0
?C.0<a<1,b>0 D.0<a<1,b<0
答案?D?
2.设指数函数f(x)=ax(a>0且a≠1),则下列等式不正确的是 ( )
? A.f(x+y)=f(x)·f(y) B.f((xy)n)=f n(x)·f n(y)
?C.f(x-y)=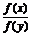 D.f(nx)=f
n(x)
D.f(nx)=f
n(x)
答案?B?
1.已知a< ,则化简
,则化简 的结果是
( )
的结果是
( )
A.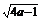 B.-
B.-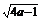 ? C.
? C. ?D.-
?D.-
答案?C?
12.设关于x的一元二次方程ax2+x+1=0(a>0)有两个实根x1,x2.
(1)求(1+x1)(1+x2)的值;
(2)求证:x1<-1且x2<-1;
(3)若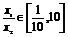 ,试求a的最大值.
,试求a的最大值.
(1)解 ∵x1、x2为方程ax2+x+1=0的两个实根,∴x1+x2=- ,x1x2=
,x1x2=
∴(1+x1)(1+x2)=1+(x1+x2)+x1x2=1- +
+ =1.
=1.
(2)证明 令f(x)=ax2+x+1,Δ=1-4a≥0得0<2a≤ ,
,
∴抛物线对称轴x=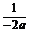 ≤-2<-1.又f(-1)=a>0.
≤-2<-1.又f(-1)=a>0.
∴f(x)图象与x轴交点均在(-1,0)的左侧,∴x1<-1且x2<-1.
(3)解 由(1)得x1= , ∴
, ∴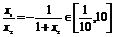
∴- ,∴a=
,∴a=
∴-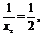 ,即x2=-2时,a的最大值为
,即x2=-2时,a的最大值为 .
.
§2.6 指数与指数函数

 基础自测
基础自测
11.f(x)=-x2+ax+ -
- 在区间[0,1]上的最大值为2,求a的值.
在区间[0,1]上的最大值为2,求a的值.
解 f(x)=-
①当 ∈[0,1],即0≤a≤2时,
∈[0,1],即0≤a≤2时,
f(x)max=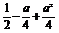 =2,则a=3或a=-2,不合题意.
=2,则a=3或a=-2,不合题意.
②当 >1,即a>2时,f(x)max=f(1)=2
>1,即a>2时,f(x)max=f(1)=2 a=
a=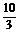 .
.
③当 <0,即a<0时,f(x)max=f(0)=2
<0,即a<0时,f(x)max=f(0)=2 a=-6,
a=-6,
∴f(x)在区间[0,1]上的最大值为2时,a=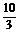 或a=-6.
或a=-6.
10.已知f(x)=x2+ax+3-a,若x∈[-2,2]时,f(x)≥0恒成立,求a的取值范围.
解 令f(x)的最小值为g(a),则
(1)当- <-2,即a>4时,g(a)=f(-2)=7-3a≥0,得a≤
<-2,即a>4时,g(a)=f(-2)=7-3a≥0,得a≤ ,又a>4,故此时a不存在;
,又a>4,故此时a不存在;
(2)当- ∈[-2,2],即-4≤a≤4时,g(a)=3-a-
∈[-2,2],即-4≤a≤4时,g(a)=3-a-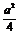 ≥0,得-6≤a≤2,又-4≤a≤4,故-4≤a≤2;
≥0,得-6≤a≤2,又-4≤a≤4,故-4≤a≤2;
(3)当- >2,即a<-4时,g(a)=f(2)=7+a≥0,得a≥-7,又a<-4,故-7≤a<-4.综上,得-7≤a≤2.
>2,即a<-4时,g(a)=f(2)=7+a≥0,得a≥-7,又a<-4,故-7≤a<-4.综上,得-7≤a≤2.
9.已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定此二次函数的解析式.
解 方法一 利用二次函数一般式.设f(x)=ax2+bx+c (a≠0),
由题意得 解之得
解之得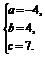 ∴所求二次函数为y=-4x2+4x+7.
∴所求二次函数为y=-4x2+4x+7.
方法二 利用二次函数顶点式.
设f(x)=a(x-m)2+n,∵f(2)=f(-1),∴抛物线对称轴为x= 即m=
即m= .
.
又根据题意函数有最大值为n=8,∴y=f(x)=a(x- )2+8.∵f(2)=-1,∴a(2-
)2+8.∵f(2)=-1,∴a(2- )2+8=-1.
)2+8=-1.
解之,得a=-4,∴y=f(x)=-4(x- )2+8=-4x2+4x+7.
)2+8=-4x2+4x+7.
方法三 由f(x)+1=0的两根为x1=2,x2=-1,故可设f(x)+1=a(x-2)(x+1),即f(x)=ax2-ax-2a-1.
又由函数有最大值ymax=8,∴ .解之,得a=-4.∴所求函数解析式为
.解之,得a=-4.∴所求函数解析式为
f (x)=a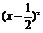 2+8=-4x222222+4x+7.
2+8=-4x222222+4x+7.
8.设函数f(x)=lg(x2+ax-a-1),给出下述命题:
①f(x)有最小值;
②当a=0时,f(x)的值域为R;
③当a>0时,f(x)在区间[2,+∞)上有反函数;
④若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围是a≥-4.
则其中正确的命题的序号是 .
答案 ②③
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com