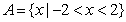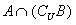1、已知集合，，全集，则等于(　　 )

A、(0,2)　 　 B、(0,2] 　 C、[0,2]　 　　　 D、[0,2)

25、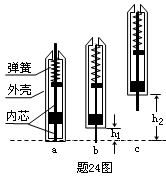(2009年重庆卷)24．探究某种笔的弹跳问题时，把笔分为轻质弹簧、内芯和外壳三部分，其中内芯和外壳质量分别为m和4m.笔的弹跳过程分为三个阶段：①把笔竖直倒立于水平硬桌面，下压外壳使其下端接触桌面(见题24图a)；②由静止释放，外壳竖直上升至下端距桌面高度为h₁时，与静止的内芯碰撞(见题24图b)；③碰后，内芯与外壳以共同的速度一起上升到外壳下端距桌面最大高度为h₂处(见题24图c)。设内芯与外壳的撞击力远大于笔所受重力、不计摩擦与空气阻力，重力加速度为g。求：

(1)外壳与内芯碰撞后瞬间的共同速度大小；

(2)从外壳离开桌面到碰撞前瞬间，弹簧做的功；

(3)从外壳下端离开桌面到上升至h₂处，笔损失的机械能。

解析：设外壳上升高度h₁时速度为V₁，外壳与内芯碰撞后瞬间的共同速度大小为V₂，

(1)对外壳和内芯，从撞后达到共同速度到上升至h₂处，应用动能定理有

(4mg+m)( h₂－h₁)＝(4m+m)V₂²，解得V₂＝；

(2)外壳和内芯，碰撞过程瞬间动量守恒，有4mV₁＝(4mg+m)V₂，

解得V₁＝，

设从外壳离开桌面到碰撞前瞬间弹簧做功为W，在此过程中，对外壳应用动能定理有

W－4mgh₁＝(4m)V₁²，

解得W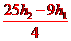＝mg；

(3)由于外壳和内芯达到共同速度后上升高度h₂的过程，机械能守恒，只是在外壳和内芯碰撞过程有能量损失，损失的能量为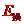＝(4m)V₁²－(4m+m)V₂²，

联立解得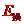＝mg(h₂－h₁)。

24、(2009年重庆卷)23．2009年中国女子冰壶队首次获得了世界锦标赛冠军，这引起了人们对冰壶运动的关注。冰壶在水平冰面上的一次滑行可简化为如下过程：如题23图，运动员将静止于O点的冰壶(视为质点)沿直线推到A点放手，此后冰壶沿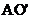滑行，最后停于C点。已知冰面与各冰壶间的动摩擦因数为μ，冰壶质量为m，AC＝L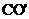，＝r,重力加速度为g ，

(1)求冰壶在A 点的速率；

(2)求冰壶从O点到A点的运动过程中受到的冲量大小；

(3)若将段冰面与冰壶间的动摩擦因数减小为，原只能滑到C点的冰壶能停于点，求A点与B点之间的距离。

答案：(1)(2)m(3)L－4r

[解析](1)对冰壶，从A点放手到停止于C点，设在A点时的速度为V₁，

应用动能定理有－μmgL＝mV₁²，解得V₁＝；

(2)对冰壶，从O到A，设冰壶受到的冲量为I，

应用动量定理有I＝mV₁－0，解得I＝m；

(3)设AB之间距离为S，对冰壶，从A到O′的过程，

应用动能定理，－μmgS－0.8μmg(L+r－S)＝0－mV₁²，

解得S＝L－4r。

23、(2009年浙江卷)24．某校物理兴趣小组决定举行遥控塞车比赛。比赛路径如图所示，赛车从起点A出发，沿水平直线轨道运动L后，出B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在光滑平直轨道上运动到C点，并能越过壕沟。已知赛车质量m＝0.1kg，通电后以额定功率ρ＝1.5W工作，进入竖直圆轨道前受到的阻值为0.3N，随后在运动中受到的阻力均可不计。图中L＝10.00m，R=0.32m，h＝1.25m,S＝1.50m。问：要使赛车完成比赛，电动机至少工作多长时间？(取g＝10 m/s²)

答案2.53s

[解析]本题考查平抛、圆周运动和功能关系。

设赛车越过壕沟需要的最小速度为v₁，由平抛运动的规律

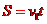
解得　　　　　　　　　

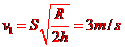
设赛车恰好越过圆轨道，对应圆轨道最高点的速度为v₂，最低点的速度为v₃，由牛顿第二定律及机械能守恒定律

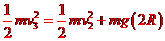
解得　　　　　　　　　　 m/s

通过分析比较，赛车要完成比赛，在进入圆轨道前的速度最小应该是

　　　　　　　　　　　　　 m/s

设电动机工作时间至少为t，根据功能原理

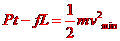
由此可得　　　　　　　　　 t=2.53s

22、(2009年天津卷)10．如图所示，质量m₁=0.3 kg 的小车静止在光滑的水平面上，车长L=15 m,现有质量m₂=0.2 kg可视为质点的物块，以水平向右的速度v₀=2 m/s从左端滑上小车，最后在车面上某处与小车保持相对静止。物块与车面间的动摩擦因数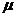=0.5,取g=10 m/s²_，求

(1)物块在车面上滑行的时间t;

(2)要使物块不从小车右端滑出，物块滑上小车左端的速度v′₀不超过多少。

答案：(1)0.24s　 (2)5m/s

[解析](1)设物块与小车的共同速度为v，以水平向右为正方向，根据动量守恒定律有

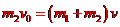　　　　　　　　　 　　　　　　　　　　　　①

设物块与车面间的滑动摩擦力为F，对物块应用动量定理有

　　　　　　　　　 　　　　　　　　　　　　②

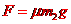其中　　　　　　　　 　　　　　　　　　　　　　　　③

解得　　　　　　　　　

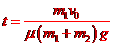
代入数据得　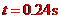　　　　　　　 　　　　　　　　　　　　　　　　　④

(2)要使物块恰好不从车厢滑出，须物块到车面右端时与小车有共同的速度v′，则

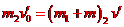　　　　　　　　　　　　 　　　　　　　　　　　　　⑤

由功能关系有

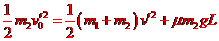　　　　　　　　　　　　 　　　　　　⑥

代入数据解得　　　　　　　 =5m/s

故要使物块不从小车右端滑出，物块滑上小车的速度v₀′不能超过5m/s。

21、(2009年四川卷)23．图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×10³ kg的重物竖直吊起的过程中，重物由静止开始向上作匀加速直线运动，加速度a=0.2 m/s²，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做v_m=1.02 m/s的匀速运动。取g=10 m/s²,不计额外功。求：

(1)　　 起重机允许输出的最大功率。

(2)　　 重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。

解析： (1)设起重机允许输出的最大功率为P₀，重物达到最大速度时，拉力F₀等于重力。

P₀＝F₀v_m①

P₀＝mg ②

代入数据，有：P₀＝5.1×10⁴W　　　　　　　　　　　　　　 ③

(2)匀加速运动结束时，起重机达到允许输出的最大功率，设此时重物受到的拉力为F，速度为v₁，匀加速运动经历时间为t₁,有：

P₀＝F₀v₁ ④

F－mg＝ma ⑤

v₁＝at₁⑥

由③④⑤⑥，代入数据，得：t₁＝5 s　　　　　　　　　　　 ⑦

T＝2 s时，重物处于匀加速运动阶段，设此时速度为v₂，输出功率为P，则

v₂＝at　　 ⑧

P＝Fv­₂⑨

由⑤⑧⑨，代入数据，得:P＝2.04×10⁴W。

20、(2009年上海物理)20．质量为5´10³ kg的汽车在t＝0时刻速度v₀＝10m/s，随后以P＝6´10⁴ W的额定功率沿平直公路继续前进，经72s达到最大速度，设汽车受恒定阻力，其大小为2.5´10³N。求：(1)汽车的最大速度v_m；(2)汽车在72s内经过的路程s。

答案：(1)24m/s(2)1252m

[解析](1)当达到最大速度时，P＝=Fv=fv_m，v_m＝＝m/s＝24m/s，

(2)从开始到72s时刻依据动能定理得：

Pt－fs＝mv_m²－mv₀²，解得：s＝＝1252m。

19、(2009年山东卷)38．(2)如图所示，光滑水平面轨道上有三个木块，A、B、C，质量分别为m_B=m_c=2m,m_A=m，A、B用细绳连接，中间有一压缩的弹簧 (弹簧与滑块不栓接)。开始时A、B以共同速度v₀运动，C静止。某时刻细绳突然断开，A、B被弹开，然后B又与C发生碰撞并粘在一起，最终三滑块速度恰好相同。求B与C碰撞前B的速度。

答案：9v₀/5

[解析]设共同速度为v，球A和B分开后，B的速度为v_B,

由动量守恒定律有,

,

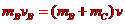联立这两式得B和C碰撞前B的速度为v_B=9v₀/5。

18、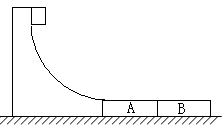(2009年山东卷)24．如图所示，某货场而将质量为m₁=100 kg的货物(可视为质点)从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物中轨道顶端无初速滑下，轨道半径R=1.8 m。地面上紧靠轨道次排放两声完全相同的木板A、B，长度均为l=2m，质量均为m₂=100 kg，木板上表面与轨道末端相切。货物与木板间的动摩擦因数为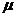₁，木板与地面间的动摩擦因数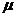=0.2。(最大静摩擦力与滑动摩擦力大小相等，取g=10 m/s²)

(1)求货物到达圆轨道末端时对轨道的压力。

(2)若货物滑上木板4时，木板不动，而滑上木板B时，木板B开始滑动，求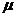_1­应满足的条件。

(3)若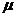₁=0。5，求货物滑到木板A末端时的速度和在木板A上运动的时间。

答案：(1)3000N；(2)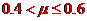；(3)0.4s

解析：(1)设货物滑到圆轨道末端是的速度为v₀，对货物的下滑过程中根据机械能守恒定律得，①，

设货物在轨道末端所受支持力的大小为F_N,根据牛顿第二定律得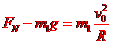，②，

联立以上两式代入数据得F_N=3000N③,

根据牛顿第三定律，货物到达圆轨道末端时对轨道的压力大小为3000N，方向竖直向下。

(2)若滑上木板A时，木板不动，由受力分析得④，

若滑上木板B时，木板B开始滑动，由受力分析得⑤，

联立④⑤式代入数据得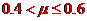⑥。

(3)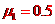，由⑥式可知，货物在木板A上滑动时，木板不动。设货物在木板A上做减速运动时的加速度大小为a₁，由牛顿第二定律得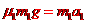⑦，

设货物滑到木板A末端是的速度为v₁，由运动学公式得⑧，

联立①⑦⑧式代入数据得v₁=4m/s⑨，

设在木板A上运动的时间为t，由运动学公式得v₁=v₀-a₁t⑩，联立①⑦⑨⑩式代入数据得t=0.4s。

17、(2009年宁夏卷)36．(2)两质量分别为M1和M2的劈A和B，高度相同，放在光滑水平面上，A和B的倾斜面都是光滑曲面，曲面下端与水平面相切，如图所示，一质量为m的物块位于劈A的倾斜面上，距水平面的高度为h。物块从静止滑下，然后双滑上劈B。求物块在B上能够达到的最大高度。

答案：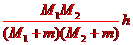

[解析]设物块到达劈A的低端时，物块和A的的速度大小分别为v和V，由机械能守恒和动量守恒得

　　　　 　　　　　　　　①

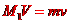　　　　 　　　　　　　　　　　　　②

设物块在劈B上达到的最大高度为，此时物块和B的共同速度大小为，由机械能守恒和动量守恒得

　　　　 　　　　③

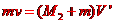　　　　 　　　　　　　　　　④

联立①②③④式得　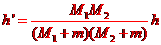　　　　　　 ⑤