例1、在正方体ABCD-A₁B₁C₁D₁中，E、F、G、H分别为棱BC、CC₁、C₁D₁、AA₁的中点，O为AC与BD的交点(如图)，求证：(1)EG∥平面BB₁D₁D；(2)平面BDF∥平面B₁D₁H；(3)A₁O⊥平面BDF；(4)平面BDF⊥平面AA₁C。

解析：

　 (1)欲证EG∥平面BB₁D₁D，须在平面BB₁D₁D内找一条与EG平行的直线，构造辅助平面BEGO’及辅助直线BO’，显然BO’即是。

　 (2)按线线平行线面平行面面平行的思路，在平面B₁D₁H内寻找B₁D₁和O’H两条关键的相交直线，转化为证明：B₁D₁∥平面BDF，O’H∥平面BDF。

(3)为证A₁O⊥平面BDF，由三垂线定理，易得BD⊥A₁O，再寻A₁O垂直于平面BDF内的另一条直线。

猜想A₁O⊥OF。借助于正方体棱长及有关线段的关系计算得：A₁O²+OF²=A₁F²A₁O⊥OF。

　 (4)∵ CC₁⊥平面AC

∴ CC₁⊥BD

又BD⊥AC

∴ BD⊥平面AA₁C

又BD平面BDF

∴ 平面BDF⊥平面AA₁C

例2、在正方体ABCD-A₁B₁C₁D₁中，M为DD₁中点，O为底面ABCD的中心，P为棱A₁B₁上任意一点，则直线OP与直线AM所成的角是

A、　　　　　 B、　　　　　 C、　　　　　 D、

解析：

取P点的特殊点A₁，连OA₁，在底面上过O作OE⊥AD于E，连A₁E

∵ OE⊥平面ADD₁A₁，AM⊥A₁E

根据三垂线定理，得：AM⊥OA₁

∴ 选D

评注：化“动”为“定”是处理“动”的思路

例3、如图，三棱锥D-ABC中，平面ABD、平面ABC均为等腰直角三角形，∠ABC=

∠BAD=90⁰，其腰BC=a，且二面角D-AB-C=60⁰。

(1)求异面直线DA与BC所成的角；

(2)求异面直线BD与AC所成的角；

(3)求D到BC的距离；

(4)求异面直线BD与AC的距离。

解析：

(1)在平面ABC内作AE∥BC，从而得∠DAE=60⁰

　∴ DA与BC成60⁰角

(2)过B作BF∥AC，交EA延长线于F，则∠DBF为BD与AC所成的角

　由△DAF易得AF=a，DA=a，∠DAF=120⁰

　∴ DF²=a²+a²-2a²·()=3a²

　∴ DF=a

△DBF中，BF=AC=a

∴ cos∠DBF=

∴ 异面直线BD与AC成角arccos

　 (3)∵ BA⊥平面ADE

∴ 平面DAE⊥平面ABC

故取AE中点M，则有DM⊥平面ABC；取BC中点N，由MN⊥BC，根据三垂线定理，DN⊥BC

∴ DN是D到BC的距离

在△DMN中，DM=a，MN=a

∴ DN=a

　 (4)∵ BF平面BDF，AC平面BDF，AC∥BF

∴ AC∥平面BDF

又BD平面BDF

∴ AC与BD的距离即AC到平面BDF的距离

∵ ，

∴

由­­，即异面直线BD与AC的距离为

评注：三棱锥的等体积变换求高，也是求点到面距离的常用方法。

例4、如图，在60⁰的二面角α-CD-β中，ACα，BDβ，且ACD=45⁰，tg∠BDC=2，CD=a，AC=x，BD=x，当x为何值时，A、B的距离最小？并求此距离。

解析：

作AE⊥CD于E，BF⊥CD于F，则EF为异面直线AE、BF的公垂段，AE与BF成60⁰角，可求得|AB|=，当x=时，|AB|有最小值。

评注：转化为求异面直线上两点间距离的最小值。

例5、如图，斜三棱柱ABC-A’B’C’中，底面是边长为a的正三角形，侧棱长为 b，侧棱AA’与底面相邻两边AB、AC都成45⁰角，求此三棱柱的侧面积和体积。

解析：

在侧面AB’内作BD⊥AA’于D

连结CD

∵ AC=AB，AD=AD，∠DAB=∠DAC=45⁰

∴ △DAB≌△DAC

∴ ∠CDA=∠BDA=90⁰，BD=CD

∴ BD⊥AA’，CD⊥AA’

∴ △DBC是斜三棱柱的直截面

在Rt△ADB中，BD=AB·sin45⁰=

∴ △DBC的周长=BD+CD+BC=(+1)a，△DBC的面积=

∴ S_侧=b(BD+DC+BC)=(+1)ab

∴ V=·AA’=

评注：求斜棱柱的侧面积有两种方法，一是判断各侧面的形状，求各侧面的面积之和，二是求直截面的周长与侧棱的乘积，求体积时同样可以利用直截面，即V=直截面面积×侧棱长。

例6、在三棱锥P-ABC中，PC=16cm，AB=18cm，PA=PB=AC=BC=17cm，求三棱锥的体积V_P-ABC。

解析：

取PC和AB的中点M和N

∴

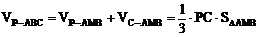
在△AMB中，AM²=BM²=17²-8²=25×9

∴ AM=BM=15cm，MN²=15²-9²=24×6

∴ S_△AMB=×AB×MN=×18×12=108(cm²)

∴ V_P-ABC=×16×108=576(cm³)

评注：把一个几何体分割成若干个三棱锥的方法是一种用得较多的分割方法，这样分割的结果，一方面便于求体积，另一方面便于利用体积的相关性质，如等底等高的锥体的体积相等，等底的两个锥体的体积的比等于相应高的比，等等。

同步练习

6、立体几何的学习，主要把握对图形的识别及变换(分割，补形，旋转等)，因此，既要熟记基本图形中元素的位置关系和度量关系，也要能在复杂背景图形中“剥出”基本图形。

5、球是由曲面围成的旋转体。研究球，主要抓球心和半径。

4、棱柱、棱锥是常见的多面体。在正棱柱中特别要运用侧面与底面垂直的性质解题，在正棱锥中，要熟记由高PO，斜高PM，侧棱PA，底面外接圆半径OA，底面内切圆半径OM，底面正多边形半边长OM，构成的三棱锥，该三棱锥四个面均为直角三角形。

3、两个重要计算公式

(1)cosθ=cosθ₁·cosθ₂

其中θ₁为斜线PA与平面α所成角，即为∠PAO，θ₂为PA射影AO与α内直线AB所成的角，θ为∠PAB。

显然，θ>θ₁，θ>θ₂

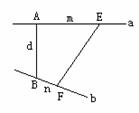
(2)异面直线上两点间距离公式

　设异面直线a，b所成角为θ

　则EF²=m²+n²+d²±2mncosθ

2、空间元素位置关系的度量

　 (1)角：异面直线所成的角，直线和平面所成的角，二面角，都化归为平面几何中两条相交直线所成的角。

异面直线所成的角：通过平移的变换手段化归，具体途径有：中位线、补形法等。

直线和平面所成的角：通过作直线射影的作图法得到。

二面角：化归为平面角的度量，化归途径有：定义法，三垂线定理法，棱的垂面法及面积射影法。

　 (2)距离：异面直线的距离，点面距离，线面距离及面面距离。

异面直线的距离：除求公垂线段长度外，通常化归为线面距离和面面距离。

线面距离，面面距离常化归为点面距离。

1、空间基本元素：直线与平面之间位置关系的小结。如下图：

条件 　结论	线线平行	线面平行	面面平行	垂直关系
线线平行	如果a∥b，b∥c，那么a∥c	如果a∥α，aβ，β∩α=b，那么a∥b	如果α∥β，α∩γ=a，β∩γ=b，那么a∥b	如果a⊥α，b⊥α，那么a∥b
线面平行	如果a∥b，aα，bα，那么a∥α	--	如果α∥β，aα，那么α∥β	--
面面平行	如果aα，bα，cβ，dβ，a∥c，b∥d，a∩b=P，那么α∥β	如果aα，bα,a∩b=P,a∥β,b∥β，那么α∥β	如果α∥β，β∥γ，那么α∥γ	如果a⊥α，a⊥β，那么α∥β

条件 　结论	线线垂直	线面垂直	面面垂直	平行关系
线线垂直	二垂线定理及逆定理	如果a⊥α，bα，那么a⊥b	如果三个平面两两垂直，那么它们交线两两垂直	如果a∥b，a⊥c，那么b⊥c
线面垂直	如果a⊥b，a⊥c，bα，cα，b∩c=P，那么a⊥α	--	如果α⊥β，α∩β=b，aα,a⊥b，那么a⊥β	如果a⊥α，b∥a，那么b⊥α
面面垂直	定义(二面角等于900)	如果a⊥α，aβ，那么β⊥α	--	--

空间几何图形的证明及计算。

(三)解答题

16、已知一个等比数列首项为1，项数是偶数，其奇数项之和为85，偶数项之和为170，求这个数列的公比和项数。

17、已知等比数列{a_n}的首项为a₁>0，公比q>-1(q≠1)，设数列{b_n}的通项b_n=a_n+1+a_n+2(n∈N₊)，数列{a_n},{b_n}的前n项和分别记为A_n，B_n，试比较A_n与B_n大小。

18、数列{a_n}中，a₁=8，a₄=2且满足a_n+2=2a_n+1-a_n(n∈N₊)

(1)求数列{a_n}通项公式；

(2)设S_n=|a₁|+|a₂|+…+|a_n|，求S_n；

(3)设(n∈N₊)T_n=b₁+b₂+…+b_n，是否存在最大的整数m，使得对于任意的n∈N₊，均有成立？若存在，求出m的值；若不存在，说明理由。

(二)填空题

11、已知数列{a_n}满足a₁+2a₂+3a₃+…+na_n=n(n+1)(n+2)，则它的前n项和S_n=______。

12、设等差数列{a_n}共有3n项，它的前2n项之和为100，后2n项之和为200，则该等差数列的中间n项的和等于________。

13、设数列{a_n}，{b_n}(b_n>0)，n∈N₊满足(n∈N₊)，则{a_n}为等差数列是{b_n}为等比数列的________条件。

14、长方体的三条棱成等比数列，若体积为216cm³，则全面积的最小值是______cm²。

15、若不等于1的三个正数a，b，c成等比数列，则(2-log_ba)(1+log_ca)=________。