
3、运算律
加法: +
+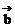 =
=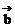 +
+ ,(
,( +
+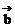 )+
)+ =
= +(
+(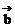 +
+ )
)
实数与向量的乘积:λ( +
+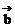 )=λ
)=λ +λ
+λ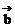 ;(λ+μ)
;(λ+μ) =λ
=λ +μ
+μ ,λ(μ
,λ(μ )=
)=
(λμ) 
两个向量的数量积: ·
·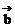 =
=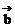 ·
· ;(λ
;(λ )·
)·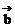 =
= ·(λ
·(λ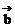 )=λ(
)=λ( ·
·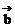 ),(
),( +
+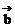 )·
)· =
= ·
· +
+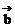 ·
·
说明:根据向量运算律可知,两个向量之间的线性运算满足实数多项式乘积的运算法则,正确迁移实数的运算性质可以简化向量的运算,例如( ±
±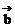 )2=
)2=
2、向量的三种线性运算及运算的三种形式。
向量的加减法,实数与向量的乘积,两个向量的数量积都称为向量的线性运算,前两者的结果是向量,两个向量数量积的结果是数量。每一种运算都可以有三种表现形式:图形、符号、坐标语言。
主要内容列表如下:
|
运
算 |
图形语言 |
符号语言 |
坐标语言 |
|
加法与减法 |
 |
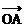 + + = =  - -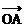 = = |
记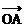 =(x1,y1), =(x1,y1), =(x1,y2) =(x1,y2)则 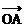 + + =(x1+x2,y1+y2) =(x1+x2,y1+y2) - -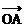 =(x2-x1,y2-y1) =(x2-x1,y2-y1) |
 |
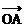 + + = = |
|
|
|
实数与向量 的乘积 |
 |
 =λ =λ λ∈R |
记 =(x,y) =(x,y)则λ  =(λx,λy) =(λx,λy) |
|
两个向量 的数量积 |
 |
 · ·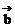 =| =| || ||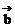 | |cos<  , ,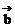 > > |
记 =(x1,y1), =(x1,y1), 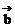 =(x2,y2) =(x2,y2)则  · ·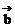 =x1x2+y1y2 =x1x2+y1y2 |
1、向量是数形结合的典范。向量的几何表示法--有向线段表示法是运用几何性质解决向量问题的基础。在向量的运算过程中,借助于图形性质不仅可以给抽象运算以直观解释,有时甚至更简捷。
向量运算中的基本图形:①向量加减法则:三角形或平行四边形;②实数与向量乘积的几何意义--共线;③定比分点基本图形--起点相同的三个向量终点共线等。
3、向量运算的运用
2、向量的线性运算:即向量的加减法,实数与向量的乘积,两个向量的数量积等的定义,运算律;
1、向量的概念;
(三) 解答题
16、若函数 的值域为[-1,5],求a,c。
的值域为[-1,5],求a,c。
17、设定义在[-2,2]上的偶函数f(x)在区间[0,2]上单调递减,若f(1-m)<f(m),求实数m的取值范围。
18、已知0<a<1,在函数y=logax(x≥1)的图象上有A,B,C三点,它们的横坐标分别是t,t+2,t+4
(1)若△ABC面积为S,求S=f(t);
(2)判断S=f(t)的单调性;
(3)求S=f(t)最大值。
19、设f(x)= ,x∈R
,x∈R
(1)证明:对任意实数a,f(x)在(-∞,+∞)上是增函数;
(2)当f(x)为奇函数时,求a;
(3)当f(x)为奇函数时,对于给定的正实数k,解不等式 。
。
20、设0<a<1,函数f(x)= 的定义域为[m,n],值[logaa(n-1),logaa(m-1)],
的定义域为[m,n],值[logaa(n-1),logaa(m-1)],
(二) 填空题
7、已知定义在R的奇函数f(x)满足f(x+2)=-f(x),且当0≤x≤1时,f(x)=x,则 =__________。
=__________。
8、 已知y=loga(2-x)是x的增函数,则a的取值范围是__________。
9、 函数f(x)定义域为[1,3],则f(x2+1)的定义域是__________。
10、函数f(x)=x2-bx+c满足f(1+x)=f(1-x),且f(0)=3,则f(bx)与f(cx)的大小关系是__________。
11、已知f(x)=log3x+3,x∈[1,9],则y=[f(x)]2+f(x2)的最大值是__________。
12、已知A={y|y=x2-4x+6,y∈N},B={y|y=-x2-2x+18,y∈N},则A∩B中所有元素的和是__________。
13、若φ(x),g(x)都是奇函数,f(x)=mφ(x)+ng(x)+2在(0,+∞)上有最大值,则f(x)在(-∞,0)上最小值为__________。
14、函数y=log2(x2+1)(x>0)的反函数是__________。
15、求值: =__________。
=__________。
(一) 选择题
1、定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上单调递增,设a=f(3),b=f( ),c=f(2),则a,b,c大小关系是
),c=f(2),则a,b,c大小关系是
A、a>b>c B、a>c>b C、b>c>a D、c>b>a
2、方程 (a>0且a≠1)的实数解的个数是
(a>0且a≠1)的实数解的个数是
A、0 B、1 C、2 D、3
3、 的单调减区间是
的单调减区间是
A、(-∞,1) B、(1,+∞) C、(-∞,-1)∪(1,+∞) D、(-∞,+∞)
3、函数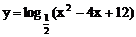 的值域为
的值域为
A、 (-∞,3] B、(-∞,-3] C、(-3,+∞) D、(3,+∞)
4、函数y=log2|ax-1|(a≠b)的图象的对称轴是直线x=2,则a等于
A、  B、
B、 C、2
D、-2
C、2
D、-2
6、有长度为24的材料用一矩形场地,中间加两隔墙,要使矩形的面积最大,则隔壁的长度为
A、 3 B、4 C、6 D、12
例1、已知 ,函数y=g(x)图象与y=f-1(x+1)的图象关于直线y=x对称,求g(11)的值。
,函数y=g(x)图象与y=f-1(x+1)的图象关于直线y=x对称,求g(11)的值。
分析:
利用数形对应的关系,可知y=g(x)是y=f-1(x+1)的反函数,从而化g(x)问题为已知f(x)。
∵ y=f-1(x+1)
∴ x+1=f(y)
∴ x=f(y)-1
∴ y=f-1(x+1)的反函数为y=f(x)-1
即 g(x)=f(x)-1
∴
g(11)=f(11)-1=
评注:函数与反函数的关系是互为逆运算的关系,当f(x)存在反函数时,若b=f(a),则a=f-1(b)。
例2、设f(x)是定义在(-∞,+∞)上的函数,对一切x∈R均有f(x)+f(x+2)=0,当-1<x≤1时,f(x)=2x-1,求当1<x≤3时,函数f(x)的解析式。
解题思路分析:
利用化归思想解题
∵ f(x)+f(x+2)=0
∴ f(x)=-f(x+2)
∵ 该式对一切x∈R成立
∴ 以x-2代x得:f(x-2)=-f[(x-2)+2]=-f(x)
当1<x≤3时,-1<x-2≤1
∴ f(x-2)=2(x-2)-1=2x-5
∴ f(x)=-f(x-2)=-2x+5
∴ f(x)=-2x+5(1<x≤3)
评注:在化归过程中,一方面要转化自变量到已知解析式的定义域,另一方面要保持对应的函数值有一定关系。在化归过程中还体现了整体思想。
例3、已知g(x)=-x2-3,f(x)是二次函数,当x∈[-1,2]时,f(x) 的最小值,且f(x)+g(x)为奇函数,求f(x)解析式。
分析:
用待定系数法求f(x)解析式
设f(x)=ax2+bx+c(a≠0)
则f(x)+g(x)=(a-1)x2+bx+c-3
由已知f(x)+g(x)为奇函数
∴ 
∴ f(x)=x2+bx+3
下面通过确定f(x)在[-1,2]上何时取最小值来确定b,分类讨论。
 ,对称轴
,对称轴
(1)当 ≥2,b≤-4时,f(x)在[-1,2]上为减函数
≥2,b≤-4时,f(x)在[-1,2]上为减函数
∴ 
∴ 2b+7=1
∴ b=3(舍)
(2)当 (-1,2),-4<b<2时
(-1,2),-4<b<2时

∴ 
∴ 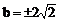 (舍负)
(舍负)
(3)当 ≤-1,b≥2时,f(x)在[-1,2]上为增函数
≤-1,b≥2时,f(x)在[-1,2]上为增函数
∴ (f(x)min=f(1)=4-b
∴ 4-b=1
∴ b=3
∴  ,或
,或
评注:二次函数在闭区间上的最值通常对对称轴与区间的位置关系进行讨论,是求值域的基本题型之一。在已知最值结果的条件下,仍需讨论何时取得最小值。
例4、定义在R上的函数y=f(x),f(0)≠0,当x>0时,f(x)>1,且对任意的a、b∈R,有f(a+b)=f(a)f(b),
(1)求证:f(0)=1;
(2)求证:对任意的x∈R,恒有f(x)>0;
(3)证明:f(x)是R上的增函数;
(4)若f(x)·f(2x-x2)>1,求x的取值范围。
分析:
(1)令a=b=0,则f(0)=[f(0)]2
∵ f(0)≠0
∴ f(0)=1
(2)令a=x,b=-x
则 f(0)=f(x)f(-x)
∴ 
由已知x>0时,f(x)>1>0
当x<0时,-x>0,f(-x)>0
∴ 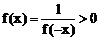
又x=0时,f(0)=1>0
∴ 对任意x∈R,f(x)>0
(3)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0
∴ 
∴ f(x2)>f(x1)
∴ f(x)在R上是增函数
(4)f(x)·f(2x-x2)=f[x+(2x-x2)]=f(-x2+3x)
又1=f(0),f(x)在R上递增
∴ 由f(3x-x2)>f(0)得:3x-x2>0
∴ 0<x<3
评注:根据f(a+b)=f(a)·f(b)是恒等式的特点,对a、b适当赋值。利用单调性的性质去掉符号“f”得到关于x的代数不等式,是处理抽象函数不等式的典型方法。
例5、已知lgx+lgy=2lg(x-2y),求 的值。
的值。
分析:
在化对数式为代数式过程中,全面挖掘x、y满足的条件
由已知得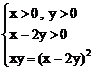
∴
x=4y,
∴

例6、某工厂今年1月,2月,3月生产某产品分别为1万件,1.2万件,1.3万件,为了估测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y与月份数x的关系,模拟函数可选用y=abx+c(其中a,b,c为常数)或二次函数,已知4月份该产品的产量为1.37万件,请问用哪个函数作为模拟函数较好?并说明理由。
分析:
设f(x)=px2+qx+r(p≠0)
则

∴

∴ f(4)=-0.05×42+0.35×4+0.7=1.3
设g(x)=abx+c
则

∴

∴ g(4)=-0.8×0.54+1.4=1.35
∵ |1.35-1.37|<|1.3-1.37|
∴ 选用y=-0.8×(0.5)x+1.4作为模拟函数较好。
巩固练习
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com