5、本章思想方法

(1)等价变换。熟练运用公式对问题进行转化，化归为熟悉的基本问题；

(2)数形结合。充分利用单位圆中的三角函数线及三角函数图象帮助解题；

(3)分类讨论。

4、三角函数的性质除了一般函数通性外，还出现了前面几种函数所没有的周期性。周期性的定义：设T为非零常数，若对f(x)定义域中的每一个x，均有f(x+T)=f(x)，则称T为f(x)的周期。当T为f(x)周期时，kT(k∈Z，k≠0)也为f(x)周期。

三角函数图象是性质的重要组成部分。利用单位圆中的三角函数线作函数图象称为几何作图法，熟练掌握平移、伸缩、振幅等变换法则。

3、三角变换公式包括和、差、倍、半公式，诱导公式是和差公式的特例，对公式要熟练地正用、逆用、变用。如倍角公式：cos2α=2cos²α-1=1-2sin²α，变形后得，可以作为降幂公式使用。

三角变换公式除用来化简三角函数式外，还为研究三角函数图象及性质做准备。

2、利用直角坐标系，可以把直角三角形中的三角函数推广到任意角的三角数。三角函数定义是本章重点，从它可以推出一些三角公式。重视用数学定义解题。

设P(x，y)是角α终边上任一点(与原点不重合)，记，则，，，。

利用三角函数定义，可以得到(1)诱导公式：即与α之间函数值关系(k∈Z)，其规律是“奇变偶不变，符号看象限”；(2)同角三角函数关系式：平方关系，倒数关系，商数关系。

1、角的概念的推广。从运动的角度，在旋转方向及旋转圈数上引进负角及大于360⁰的角。这样一来，在直角坐标系中，当角的终边确定时，其大小不一定(通常把角的始边放在x轴正半轴上，角的顶点与原点重合，下同)。为了把握这些角之间的联系，引进终边相同的角的概念，凡是与终边α相同的角，都可以表示成k·360⁰+α的形式，特例，终边在x轴上的角集合{α|α=k·180⁰，k∈Z}，终边在y轴上的角集合{α|α=k·180⁰+90⁰，k∈Z}，终边在坐标轴上的角的集合{α|α=k·90⁰，k∈Z}。

在已知三角函数值的大小求角的大小时，通常先确定角的终边位置，然后再确定大小。

弧度制是角的度量的重要表示法，能正确地进行弧度与角度的换算，熟记特殊角的弧度制。在弧度制下，扇形弧长公式l=|α|R，扇形面积公式，其中α为弧所对圆心角的弧度数。

3、三角函数的图象及性质。

2、三角公式，包括诱导公式，同角三角函数关系式和差倍半公式等；

1、三角函数的概念及象限角、弧度制等概念；

(三)解答题

　　 20、某天的课程表要排入政治、语文、数学、物理、体育、美术共6节课，如果第1节不排体育，最后1节不排数学，那么共有多少种不同的排课表的方法。

21、有甲、乙、丙三位老师，分到6个班上课：

(1)每人上2个班课，有多少种分法？

(2)甲、乙都上1个班课，丙上4个班课，有多少种分法？

(3)2人各上1个班课，1个人上4个班课，有多少种分法？

　　 22、在x(1-x)^k+x²(1+2x)⁸+x³(1+3x)¹²的展开式中，含x⁴的系数是144，求k的值并求出含x²项的系数等于多少？

23、某气象站天气预报的准确率为80%，求：

　 (1)5次预报中恰有4次准确的概率；

　 (2)5次预报中至少有4次准确的概率(结果保留2位有效数字)。

24、有6个房间安排4个旅游者住，每人可以进住任一房间，且进住房间是等可能的，试求下列事件的概率：

(1)事件A：指定的4个房间各有1人；

(2)事件B：恰有4个房间中各有1人；

(3)事件C：指定的某个房间中有2人；

(4)事件D：第1号房间有1人，第2号房间有3人。

25、有甲、乙两批种子，发芽率分别为0.8，0.7，从两批种子中各取1粒，求：

　 　(1)2粒种子都能发芽的概率；

　 (2)至少有1粒种子发芽的概率；

　 (3)恰好有1粒种子发芽的概率。

26、如图构成系统的每个元件的可靠性为r(0<r，r<1)，且各个元件能否正常工作是相互独立的，试求图中两种系统的可靠性。

(二)填空题

15、空间12个点，其中5个点共面，此外无任何4个点共面，这12个点最多可决定_________个不同的平面。

16、(4+2x+x²)(2-x)⁷展开式中x⁵的系数为________。

17、=__________。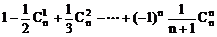

18、有1个数字难题，在半小时内，甲能解决它的概率是，乙能解决它的概率是，两人试图独立地在半小时内解决它，则：

(1)两人都未解决的概率为__________；

(2)问题得到解决的概率为__________。

19、一次考试出了10个选择题，每道题有4个可供选择的答案，其中1个是正确的，3个是错误的，某学生只知道5个题的正确答案，对其他5个题全靠猜回答，那么这个学生卷面上正确答案不少于7个题的概率是________________。