
5. ⑴复数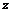 是实数及纯虚数的充要条件:
是实数及纯虚数的充要条件:
①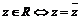 .
.
②若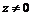 ,
,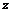 是纯虚数
是纯虚数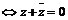 .
.
⑵模相等且方向相同的向量,不管它的起点在哪里,都认为是相等的,而相等的向量表示同一复数. 特例:零向量的方向是任意的,其模为零.
注: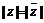 .
.
4. ⑴①复数的乘方: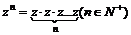
②对任何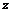 ,
,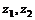
 及
及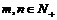 有
有
③
注:①以上结论不能拓展到分数指数幂的形式,否则会得到荒谬的结果,如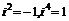 若由
若由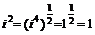 就会得到
就会得到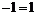 的错误结论.
的错误结论.
②在实数集成立的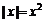 . 当
. 当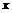 为虚数时,
为虚数时,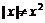 ,所以复数集内解方程不能采用两边平方法.
,所以复数集内解方程不能采用两边平方法.
⑵常用的结论:
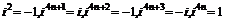
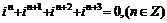
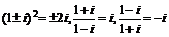
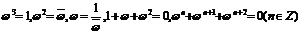 若
若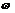 是1的立方虚数根,即
是1的立方虚数根,即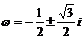 ,则
.
,则
.
3. 共轭复数的性质:
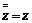
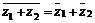
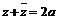 ,
,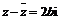 (
(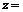 a + bi)
a + bi)
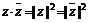
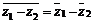
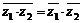
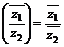 (
(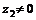 )
)
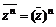
注:两个共轭复数之差是纯虚数. (×)[之差可能为零,此时两个复数是相等的]
2. ⑴复平面内的两点间距离公式: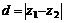 .
.
其中 是复平面内的两点
是复平面内的两点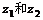 所对应的复数,
所对应的复数,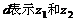 间的距离.
间的距离.
由上可得:复平面内以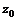 为圆心,
为圆心,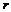 为半径的圆的复数方程:
为半径的圆的复数方程: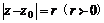 .
.
⑵曲线方程的复数形式:
①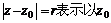 为圆心,r为半径的圆的方程.
为圆心,r为半径的圆的方程.
②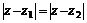 表示线段
表示线段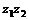 的垂直平分线的方程.
的垂直平分线的方程.
③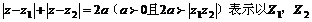 为焦点,长半轴长为a的椭圆的方程(若
为焦点,长半轴长为a的椭圆的方程(若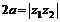 ,此方程表示线段
,此方程表示线段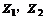 ).
).
④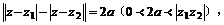 表示以
表示以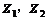 为焦点,实半轴长为a的双曲线方程(若
为焦点,实半轴长为a的双曲线方程(若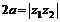 ,此方程表示两条射线).
,此方程表示两条射线).
⑶绝对值不等式:
设 是不等于零的复数,则
是不等于零的复数,则
①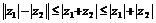 .
.
左边取等号的条件是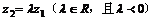 ,右边取等号的条件是
,右边取等号的条件是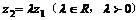 .
.
②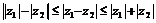 .
.
左边取等号的条件是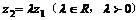 ,右边取等号的条件是
,右边取等号的条件是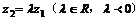 .
.
注: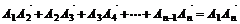 .
.
1. ⑴复数的单位为i,它的平方等于-1,即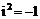 .
.
⑵复数及其相关概念:
①
复数-形如a + bi的数(其中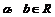 );
);
② 实数-当b = 0时的复数a + bi,即a;
③
虚数-当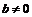 时的复数a + bi;
时的复数a + bi;
④
纯虚数-当a = 0且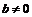 时的复数a + bi,即bi.
时的复数a + bi,即bi.
⑤ 复数a + bi的实部与虚部-a叫做复数的实部,b叫做虚部(注意a,b都是实数)
⑥ 复数集C-全体复数的集合,一般用字母C表示.
⑶两个复数相等的定义:
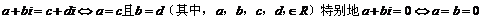 .
.
⑷两个复数,如果不全是实数,就不能比较大小.
注:①若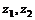 为复数,则
为复数,则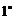 若
若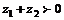 ,则
,则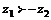 .(×)[
.(×)[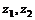 为复数,而不是实数]
为复数,而不是实数]
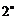 若
若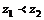 ,则
,则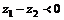 .(√)
.(√)
②若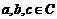 ,则
,则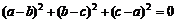 是
是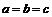 的必要不充分条件.(当
的必要不充分条件.(当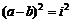 ,
,
 时,上式成立)
时,上式成立)
10. 将in划去
9. question - questions
8. 在They后加were
7. have -had
5. his - their
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com